
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывность функции
Понятие непрерывности функции интуитивно связано с непрерывностью линии (графика функции). С точки зрения математика это понятие связано с существованием предела функции в точке.

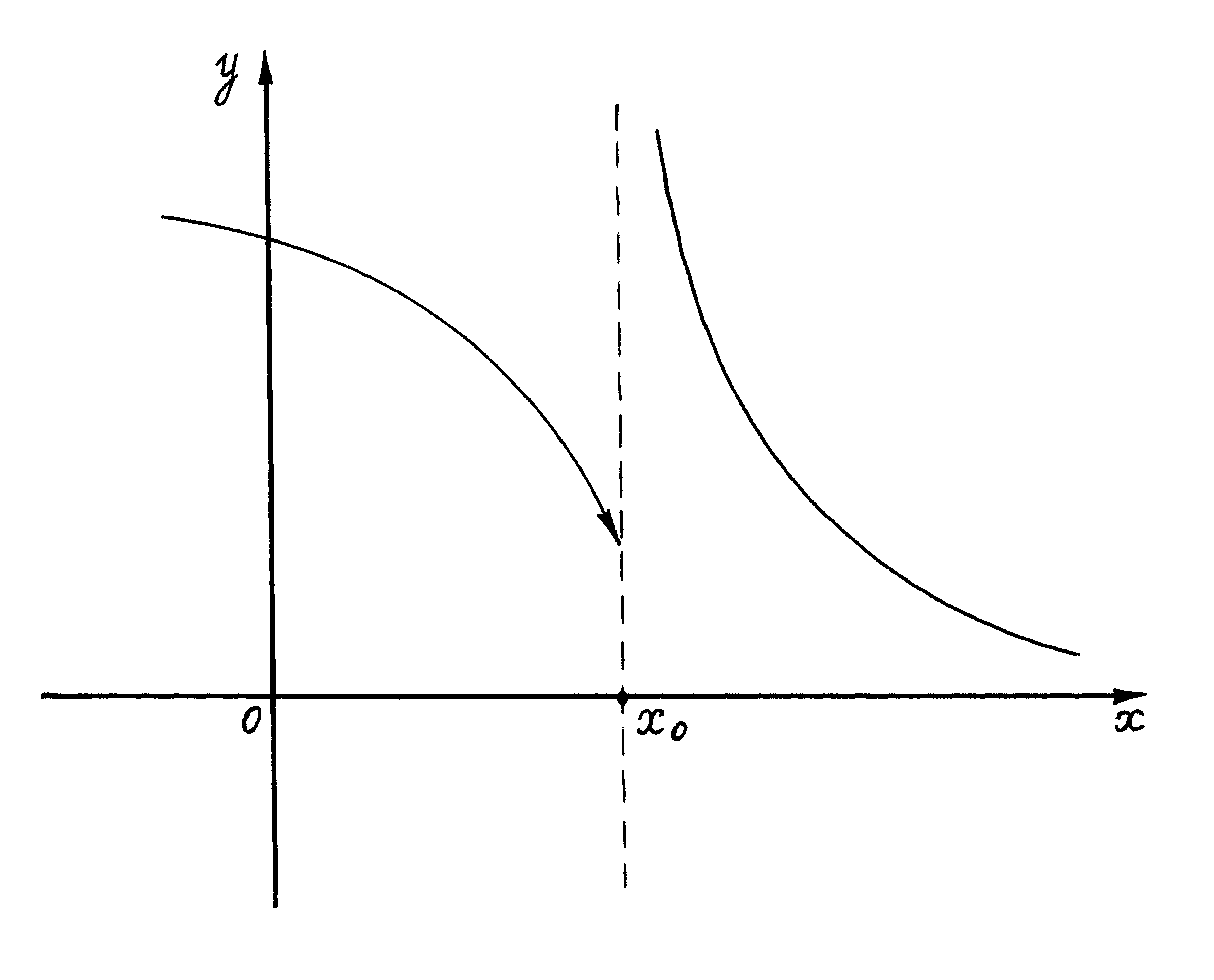
Рис. 17. Рис. 18
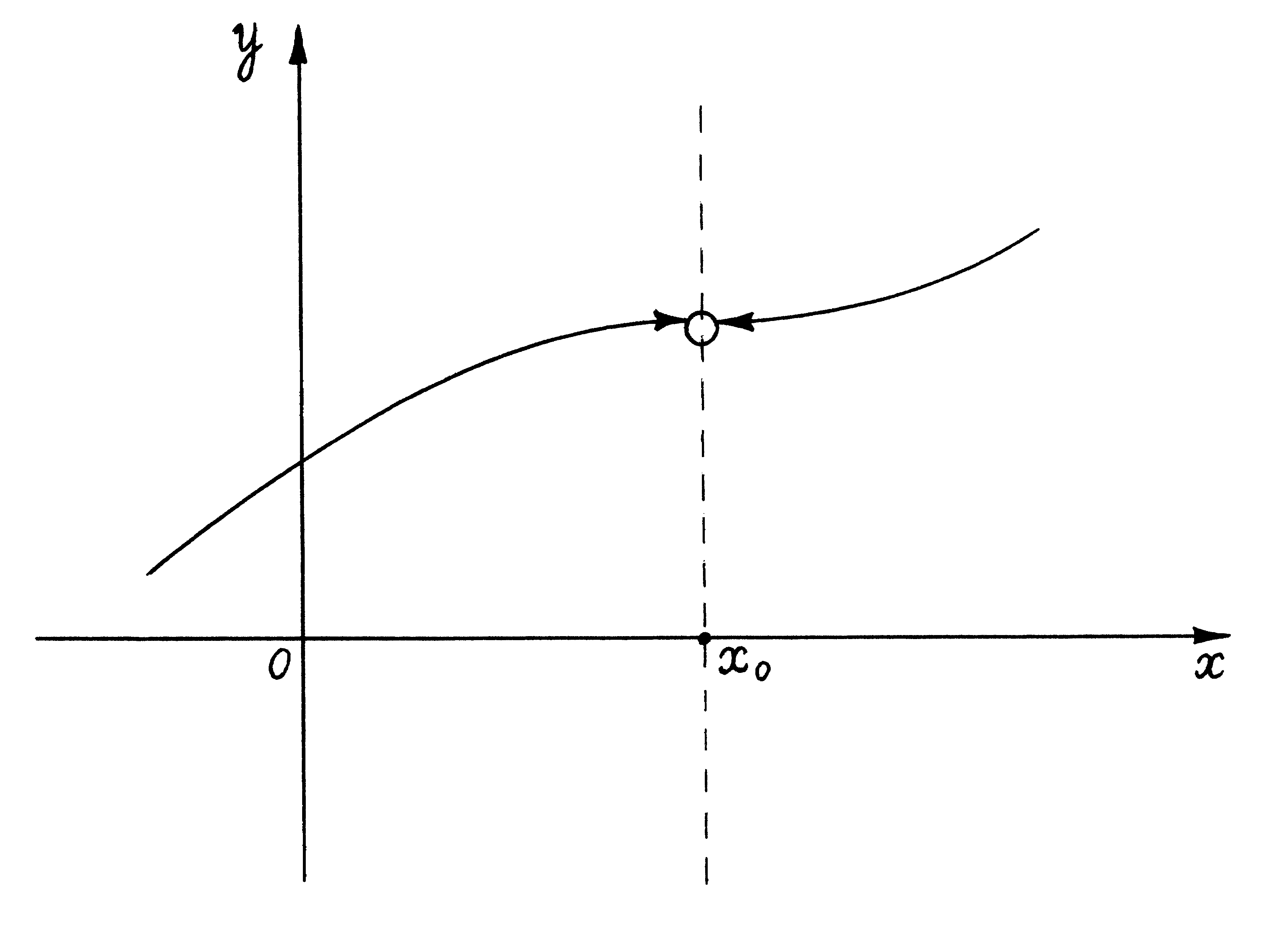

. Рис. 19. Рис. 20.
На рисунках 17–20 представлены графики различных функций, из которых только одна (рис. 20) является непрерывной в точке х0. Остальные функции не являются непрерывными в точке по разным причинам. На рис. 17 дан график функции, которая имеет в точке х0 различные (хотя и конечные) односторонние пределы. На рис. 18 функция в точке х0 не имеет конечного правого предела. На рис. 19 функция имеет оба равные односторонние пределы, но сама в точке х0 не определена. Таким образом, для непрерывности функции в точке должны быть устранены все эти особенности.
Определение.Функция ƒ(х) называется непрерывной в точке х0, если
1) она определена в точке х0 и в некоторой ее окрестности,
2) существует 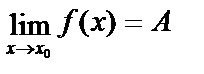 ,
,
3) предел функции в точке х0 равен значению функции в
этой точке, т. е. 
Второе условие определения может быть сформулировано более подробно: существуют и равны оба односторонних предела в точке, т. е.
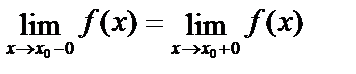
Рассмотрим примеры.
№ 1. 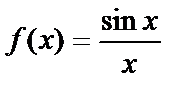 .
.
Эта функция не является непрерывной в точке х=0, т. к. в этой точке она не определена.
№ 2. 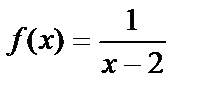 .
.
Эта функция не является непрерывной в точке х=2, т. к. в этой точке не существует ее предел: 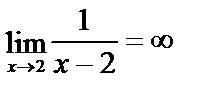 .
.
Заметим, что 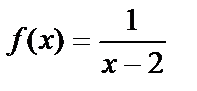 в точке х=2 тоже не определена.
в точке х=2 тоже не определена.
№ 3. Зададим функцию с помощью двух аналитических выражений, а именно
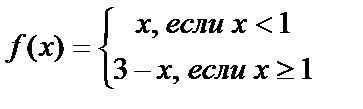
Посмотрим, является ли эта функция непрерывной в точке х=1. Значение функции в этой точке ƒ(1)=3–1=2. Функция определена для всех действительных чисел.
Вычислим односторонние пределы. При х < 1 ƒ(х)=х, поэтому
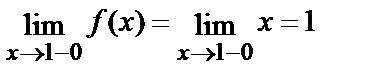
При х > 1 ƒ(х)=3–х, поэтому
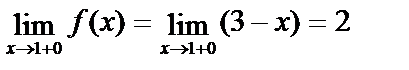
Так как односторонние пределы не равны между собой, то не существует  и в точке х=1 функция не может быть непрерывной.
и в точке х=1 функция не может быть непрерывной.
Определение. Функция называется непрерывной на отрезке, если она
непрерывна в каждой точке этого отрезка.
Рассматривая простейшие элементарные функции, легко убедится, что каждая из них непрерывна в области своего определения.
Определение.Точка х=х0 называется точкой разрыва функции, если в
этой точке нарушается хотя бы одно требование
непрерывности.
На рисунках 17–19 приведены примеры точек разрыва.
Точку называют точкой разрыва первого рода, если существуют и конечны оба односторонних предела.
Точку разрыва называют точкой разрыва второго рода, если хотя бы один односторонний предел в этой точке не существует (или бесконечен).
В рассмотренном примере № 3 функция 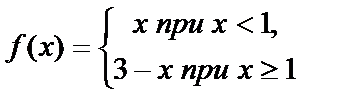 имеет в точке х=1 точку разрыва первого рода.
имеет в точке х=1 точку разрыва первого рода.
График этой функции состоит из двух полупрямых у=х (для х < 1) и у=3–х (для х ³ 1).
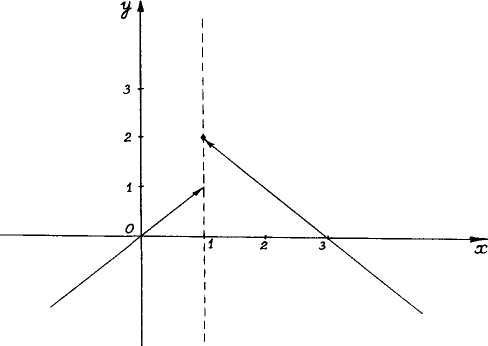
Рис. 21.
При исследовании функции на непрерывность точку разрыва следует искать там, где функция не определена, или в точках, где одно аналитическое выражение функции меняется на другое.
Укажем некоторые свойства непрерывных функций.
1. Если функции ƒ(х) и φ(х) непрерывны в точке х0, то непрерывны в точке х0 функции ƒ(х)±φ(х), ƒ(х)·φ(х), 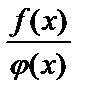 .
.
Заметим, что 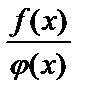 непрерывна в точке х0 только, если φ(х0)¹0.
непрерывна в точке х0 только, если φ(х0)¹0.
2. Каждая элементарная функция непрерывна в своей области определения.
3. Непрерывная на отрезке функция принимает на этом отрезке свое наибольшее и свое наименьшее значения.
4. Если функция ƒ(х) непрерывна на отрезке [а, b] и ƒ(а)=А, ƒ(b)=В, то каково бы ни было число С (А < С < В), найдется точка х=с внутри отрезка [а, b] такая, что
ƒ(с)=С
То есть функция принимает на отрезке все промежуточные значения.
5. Если функция ƒ(х) непрерывна на отрезке [а, b] и принимает на концах его значения разных знаков (ƒ(а)·ƒ(b) < 0), то внутри отрезка найдется точка х=с такая, что ƒ(с)=0. Это свойство позволяет приближенно находить корень уравнения, т. к. если ƒ(с)=0, то с – решение уравнения ƒ(х)=0.
Дата добавления: 2015-01-05; просмотров: 261; Мы поможем в написании вашей работы!; Нарушение авторских прав |