
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциальное исчисление функций одной переменной
Производной  функции
функции  в точке
в точке 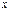 называется: предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
называется: предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю: 
Функция, имеющая производную в рассматриваемой точке, называется дифференцируемой
Если функция дифференцируема в точке  , то она непрерывна
, то она непрерывна
Если непрерывная функция  имеет производную
имеет производную  в точке
в точке 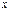 , то ее график имеет касательную, угловой коэффициент которой равен :
, то ее график имеет касательную, угловой коэффициент которой равен : 
Уравнение касательной к графику функции  в точке
в точке  имеет вид:
имеет вид:
y=f(x0)+f '(x0)(x-x0) или y-y0=y'0 (x-x0)
Производная функции  , выражающей закон движения точки по прямой
, выражающей закон движения точки по прямой  , равна
, равна 
Нахождение производных функций называется дифференцированием
 U '(x)±V '(x)
U '(x)±V '(x)
 C×U '(x)
C×U '(x)
 U '(x)×V(x) + U(x)×V '(x)
U '(x)×V(x) + U(x)×V '(x)

Производная сложной функции: если  , а
, а  и обе функции дифференцируемы, то
и обе функции дифференцируемы, то
y'x=y'u×u'x
 0
0
 a×x a-1
a×x a-1
 ax×lna
ax×lna
 ex
ex
 1
1




 cosx
cosx
 -sinx
-sinx























 -12sin3x×cos3x
-12sin3x×cos3x




 6ctg2x
6ctg2x

 445
445
 , то
, то 
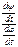

 ,
, 

Дифференциалом функции в данной точке называется главная часть приращения функции

Если функция 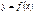 имеет в точке
имеет в точке  конечную производную
конечную производную  , то ее приращение может быть представлено в виде
, то ее приращение может быть представлено в виде 
Найти дифференциал функции  y'=12x3+12x
y'=12x3+12x

 du ± dv
du ± dv
 v×du + u×dv
v×du + u×dv
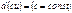 c×du
c×du


Найти дифференциал функции 

 ,
, 




Найти  от
от 

С точки зрения физики вторая производная от пути по времени равна ускорению
Найти  от
от  y'''=6ex+6xex+x2ex
y'''=6ex+6xex+x2ex

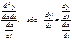
Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от  y'''=8cos(x)sin(x)
y'''=8cos(x)sin(x)
Найти  от
от 

Найти  от
от  d2y = 6+4e2x
d2y = 6+4e2x
Пусть функция 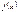 определена и непрерывна на отрезке
определена и непрерывна на отрезке 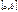 , если она дифференцируема во всех внутренних точках отрезка, а на концах отрезка имеет одинаковые значения, т.е.
, если она дифференцируема во всех внутренних точках отрезка, а на концах отрезка имеет одинаковые значения, т.е.  , то внутри отрезка найдется по крайней мере одна точка
, то внутри отрезка найдется по крайней мере одна точка  , в которой производная равна нулю:
, в которой производная равна нулю: 
Пусть функция 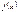 определена и непрерывна на отрезке
определена и непрерывна на отрезке  , если она дифференцируема во всех внутренних точках отрезка, то внутри найдется по крайней мере одна точка
, если она дифференцируема во всех внутренних точках отрезка, то внутри найдется по крайней мере одна точка  , что будет выполняться
, что будет выполняться
соотношение: f(b)-f(a)=f '(x0)(b-a)
Пусть функции 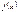 и
и  определены и непрерывны на отрезке
определены и непрерывны на отрезке 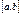 . Если они дифференцируемы во всех внутренних точках отрезка, причем
. Если они дифференцируемы во всех внутренних точках отрезка, причем  в этих точках, то внутри отрезка найдется хотя бы одна точка
в этих точках, то внутри отрезка найдется хотя бы одна точка  , что будет выполняться соотношение:
, что будет выполняться соотношение: 
Пусть функция 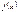 определена и непрерывна на отрезке
определена и непрерывна на отрезке  и принимает свое наибольшее (или наименьшее) значение в некоторой внутренней точке
и принимает свое наибольшее (или наименьшее) значение в некоторой внутренней точке  этого отрезка. Если функция дифференцируема в точке
этого отрезка. Если функция дифференцируема в точке  , то f '(x0)=0
, то f '(x0)=0
Функция  возрастает на интервале
возрастает на интервале  , если f '(x)>0
, если f '(x)>0
Функция  убывает на интервале
убывает на интервале  , если f '(x)<0
, если f '(x)<0
Найти интервал возрастания функции  [1;µ)
[1;µ)
$$
Найти интервал убывания функции  (-µ;1]
(-µ;1]
Точка  называется точкой строгого локального максимума функции
называется точкой строгого локального максимума функции  , если для всех
, если для всех  из некоторой окрестности
из некоторой окрестности  выполняется f(x0+Dx)-f(x0)<0
выполняется f(x0+Dx)-f(x0)<0
Точка  называется точкой строгого локального минимума функции
называется точкой строгого локального минимума функции  , если для всех
, если для всех  из некоторой окрестности
из некоторой окрестности  выполняется f(x0+Dx)-f(x0)>0
выполняется f(x0+Dx)-f(x0)>0
Точки, в которых производная данной функции равна или не существует, называются экстремумами или критическими
Пусть  - критическая точка функции
- критическая точка функции 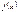 . Тогда, если в некоторой окрестности точки
. Тогда, если в некоторой окрестности точки  слева и справа от этой точки
слева и справа от этой точки  имеет разные знаки, причем если слева от точки
имеет разные знаки, причем если слева от точки  , а справа
, а справа  , то
, то  - точка экстремума, а именно максимум
- точка экстремума, а именно максимум
Пусть  - критическая точка функции
- критическая точка функции  . Тогда, если в некоторой окрестности точки
. Тогда, если в некоторой окрестности точки  слева и справа от этой точки
слева и справа от этой точки  имеет разные знаки, причем если слева от точки
имеет разные знаки, причем если слева от точки  , а справа
, а справа  , то
, то  - точка экстремума, а именно минимум
- точка экстремума, а именно минимум
Найти экстремумы функции  x = -2
x = -2
Если  , то критическая точка
, то критическая точка  является точкой экстремума функции
является точкой экстремума функции 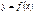 . При этом если
. При этом если  , то
, то  минимум
минимум
Если  , то критическая точка
, то критическая точка  является точкой экстремума функции
является точкой экстремума функции 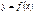 . При этом если
. При этом если  , то
, то  максимум
максимум
Используя второй достаточный признак экстремума, найти экстремум функции 
x1=0 - максимум, x2=2 - минимум
Исследовать на экстремум функцию  x1=-2 - максимум, x2=3 - минимум
x1=-2 - максимум, x2=3 - минимум
Найти интервалы возрастания функции  (-µ;-2)U(3; µ)
(-µ;-2)U(3; µ)
Найти интервалы убывания функции  (-2;3)
(-2;3)
Найти наибольшее и наименьшее значение функции 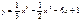 на отрезке
на отрезке 
ymax(0)=1, ymin(3) = -12.5
Если функция 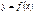 имеет на интервале
имеет на интервале  вторую производную и
вторую производную и  во всех точках
во всех точках  , то график функции вогнут
, то график функции вогнут
Если функция 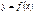 имеет на интервале
имеет на интервале  вторую производную и
вторую производную и  во всех точках
во всех точках  , то график функции выпукл
, то график функции выпукл
Найти точки перегиба графика функции  x =
x =
Найти интервал выпуклого графика функции  (-µ;1)
(-µ;1)
Найти интервал вогнутости графика функции  (1; µ)
(1; µ)
Найти точки перегиба графика функции  x=0
x=0
Найти интервал вогнутости графика функции  (-µ;0)
(-µ;0)
Найти интервал выпуклости графика функции  (0; µ)
(0; µ)
Найти вертикальную асимптоту для графика функции  x=1
x=1
Найти вертикальную асимптоту для графика функции  x=1
x=1
Найти вертикальную асимптоту для графика функции  x=-1
x=-1
Выяснить, имеет ли график функции  наклонные асимптоты y = x
наклонные асимптоты y = x
Найти наклонные асимптоты графика функции  их нет
их нет
Выяснить вопрос о наличии наклонной асимптоты у графика функции  их нет
их нет
Найти предел по правилу Лопиталя  8/5
8/5
Найти предел по правилу Лопиталя 
Найти предел по правилу Лопиталя  µ
µ
Найти предел по правилу Лопиталя 
Найти предел по правилу Лопиталя  /2
/2
Найти предел по правилу Лопиталя  µ
µ
Найти  от
от 

Найти  от
от 
 512
512
Найти  от
от  y'(x) = -x2e-x
y'(x) = -x2e-x
Найти  от
от  y'(x) = x2cosx
y'(x) = x2cosx
Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 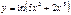

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 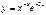

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти  от
от 

Найти производную  от неявной функции
от неявной функции 
Найти  от неявной функции
от неявной функции 

Найти  от неявной функции
от неявной функции 

Найти  от неявной функции
от неявной функции 

Найти  от неявной функции
от неявной функции 

Найти  от неявной функции
от неявной функции 

Найти  от неявной функции
от неявной функции 

Найти  от неявной функции
от неявной функции 

Найти производную от функции, заданной параметрически 

Найти производную от функции, заданной параметрически 

Найти производную от функции, заданной параметрически 

Найти производную от функции, заданной параметрически 

Найти производную от функции, заданной параметрически 

Найти производную второго порядка от 

Найти  от
от 

Найти  от
от 

Найти производную  обратной функции
обратной функции 

Найти производную  обратной функции
обратной функции 

Дата добавления: 2015-01-05; просмотров: 327; Мы поможем в написании вашей работы!; Нарушение авторских прав |