
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тесты по интегральному исчислению функции одной переменной
Функция 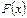 называется первообразной функции
называется первообразной функции  на промежутке
на промежутке 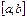 , если функция
, если функция 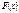 дифференцируема на
дифференцируема на 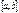 и выполняется равенство f(x)=F'(x)
и выполняется равенство f(x)=F'(x)
 F(x)+C
F(x)+C
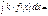


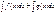
Если 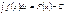 , то
, то 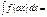 aF(x)+C
aF(x)+C
Если 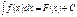 , то
, то 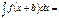 F(x)+bx+C
F(x)+bx+C
Если  , то
, то  aF(x)+bx+C
aF(x)+bx+C
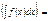 f(x)
f(x)
Если 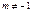 , то
, то 
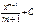
Если 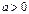 ,
,  , то
, то 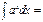
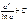
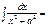
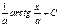
Если 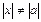 , то
, то 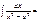
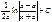
Если 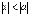 , то
, то 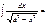
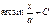
Если 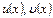 - дифференцируемые функции, то
- дифференцируемые функции, то 
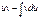
 tgx +С
tgx +С
 -ctgx +C
-ctgx +C


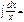 lnx+C
lnx+C
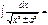
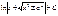
Определенный интеграл функции 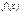 на отрезке
на отрезке  равен пределу
равен пределу 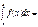
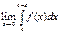
Чтобы функция 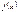 была интегрируемой на отрезке
была интегрируемой на отрезке 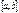 , она должна быть непрерывной
, она должна быть непрерывной
Если функция 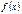 интегрируема на наибольшем из отрезков
интегрируема на наибольшем из отрезков 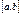 ,
, 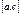 и
и  , то
, то 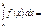
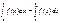
Если функции  ,
, 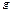 интегрируемы на
интегрируемы на 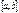 и
и  , то
, то 
Если функция 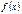 непрерывна на
непрерывна на  и функция
и функция 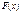 некоторая ее первообразная, то
некоторая ее первообразная, то
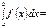 F(b) – F(a)
F(b) – F(a)
Если функция 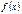 четная, то
четная, то  2F(a)
2F(a)
Если функция 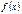 нечетная, то
нечетная, то 
Несобственный интеграл-го рода 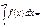
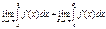
Если функции 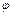 ,
, 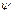 в параметрических уравнениях кривой
в параметрических уравнениях кривой  непрерывны на
непрерывны на 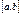 , то
, то 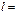
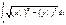
Если кривая  задана уравнением
задана уравнением  , тогда
, тогда 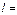
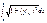
Если кривая  задана полярным уравнением
задана полярным уравнением  ,
,  , то
, то 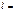
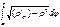
Если знак функции 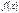 меняется на
меняется на 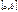 конечное число раз, то площадь
конечное число раз, то площадь 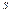 плоской фигуры, ограниченной линиями
плоской фигуры, ограниченной линиями 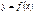 ,
, 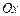 ,
,  ,
,  , равна
, равна 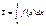
Площадь плоской фигуры, ограниченной линиями  ,
, 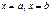 ,
,  , равна
, равна
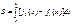
Площадь плоской фигуры, ограниченной линией  , равна
, равна 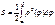
Площадь плоской фигуры, ограниченной линией, заданной параметрическими уравнениями 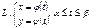 , равна
, равна 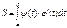
Объем тела, образованного вращением кривой  вокруг оси
вокруг оси 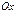 ,
,  равен
равен 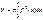
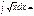
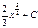
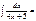

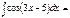

 cos(-5+x) + C
cos(-5+x) + C
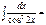
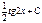
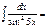
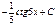
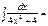

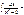
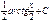
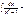 arctgx + C
arctgx + C
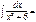



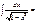 arcsinx + C
arcsinx + C

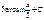
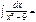

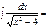
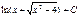

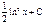

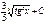
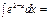
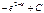

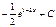
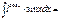
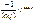
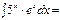
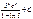
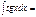 -ln(cosx) + C
-ln(cosx) + C
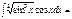
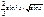
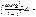

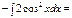 -cosx∙sinx – x + C
-cosx∙sinx – x + C
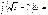
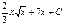

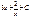
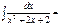 arctg(1+x) + C
arctg(1+x) + C

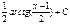
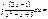 ln(x2-x+5)
ln(x2-x+5)

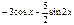
 ln(2x2-3x-7)
ln(2x2-3x-7)


 ln(x2+11)
ln(x2+11)
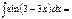
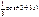
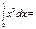 1/4
1/4
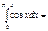 1/
1/ 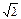
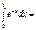 -e-1+1
-e-1+1

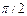
 0
0
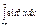
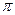
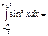
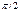
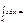 0
0
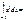 16/3
16/3
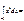 0
0
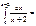 1-ln2
1-ln2
 0
0
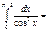

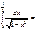
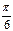
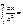 1
1
Найти площадь плоской фигуры, ограниченной линиями 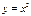 ,
, 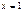 ,
,  S=1/3
S=1/3
Найти площадь плоской фигуры, ограниченной линиями 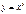 ,
,  ,
, 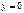 S=1/4
S=1/4
Найти площадь плоской фигуры, ограниченной линиями 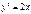 ,
,  ,
, 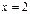 S=8/3
S=8/3
Найти площадь плоской фигуры, ограниченной линиями  ,
, 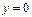 ,
, 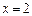 S=8
S=8 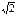 /3
/3
Найти площадь плоской фигуры, ограниченной линией 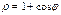

Найти площадь плоской фигуры, ограниченной линией 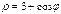
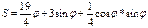
Найти площадь плоской фигуры, ограниченной линией 

Найти площадь плоской фигуры, ограниченной линией 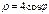
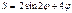
Найти площадь плоской фигуры, ограниченной линией  ,
, 

Найти площадь плоской фигуры, ограниченной линией 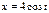 ,
, 
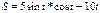
Найти площадь плоской фигуры, ограниченной линией 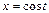 ,
, 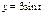

Найти площадь плоской фигуры, ограниченной линией 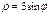
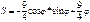
Найти длину дуги кривой 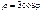
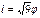
Найти длину дуги кривой 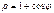
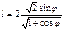
Найти длину дуги кривой 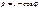
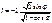
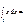



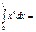

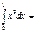
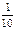
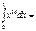

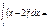

 0
0
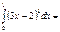
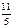
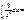 0
0
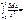

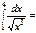 1
1
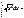
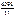
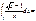 4 – 2 * ln
4 – 2 * ln
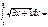



 2
2
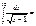 2
2
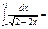
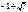
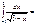 2
2
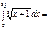 52,5
52,5
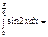
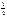
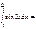
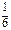
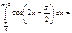

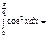
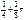
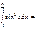

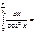

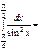

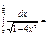
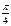
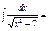


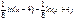
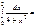


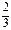
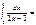
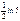
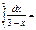
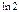
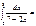
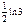
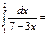
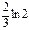
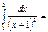
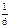
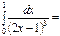
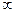
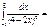
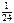
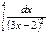 =
= 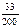
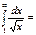
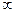
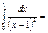
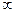
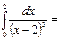 -
- 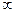

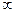

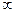
Найти длину дуги кривой  ,
, 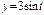
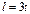
Найти длину дуги кривой 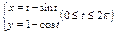
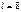
Найти длину дуги кривой 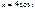 ,
, 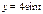

Найти длину дуги кривой 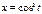 ,
, 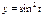
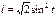
Найти длину дуги кривой  ,
,
Дата добавления: 2015-01-05; просмотров: 383; Мы поможем в написании вашей работы!; Нарушение авторских прав |