
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод стандартных передаточных функций
Стандартная передаточная функция (СПФ) разомкнутого контура WСТ(р) обладает необходимым порядком астатизма и включает параметр а0 = r0/tp, который обеспечивает заданное быстродействие через константу r0, причём последняя берётся из табл. 9. Величина перерегулирования s% обеспечи-
Таблица 9
| N | M | n | s% | К | WСТ(р) | r0 |
| a0/1,4 | а20/(p2 + 1,4 a0p) | |||||
| a0/2 | a30/(p3 + 2a0p2 + 2a20 p) | |||||
| a0/2,6 | A40/(p4 + 2,6 a0 p3 + 3,4 a30 p2 + 2,6 a0 p) |
Относительное время переходного процесса r0 = a0 tp .
вается подбором коэффициентов СПФ. Считается, что передаточная функция неизменяемой части WH(p) известна, а точность управления, время регулирования tp и величина перерегулирования s% заданы. Структуру корректирующего устройства WКУ(р) определяют из равенства
WH(p) WКУ(р) = WСТ(р),
откуда
WКУ(p) = W-1 Н(р) * WСТ(р),
или выбирают на основе опыта эксплуатации подобных систем. В некоторых случаях удается добиться полного выполнения равенства.
Реакция замкнутой системы на входное воздействие определяется распределением корней числителя (нулей) и знаменателя (полюсов) передаточной функции. Очевидно, что может быть найдено некоторое "оптимальное" распределение их на комплексной плоскости, при котором переходная функция будет наилучшей с точки зрения динамики рассматриваемой системы. Каждому такому распределению соответствует и вполне определённые значения коэффициентов передаточной функции, которые называются стандартными.
Пусть характеристический полином замкнутого контура представлен в виде
G(p) = a0pn + a1pn-1 + ... + an .
Приведём его к виду
G(p) = pn + A1w0 pn-1 + ... + An-1w0n-1p + w0n,
где w0 = 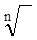 (an/a0) - собственная частота системы;
(an/a0) - собственная частота системы;
A1 = a1/(a0 w); A2 = a2/(a0 w02); ...; An-1 = an-1/(a0 w0n.
При этом нормированное значение длительности переходного процесса τ и время регулирования реальной tp системы связаны соотношением
ω0 = τ / tp .
В качестве типовых можно взять передаточные функции
W(p) = w0n/(pn + A1w0 pn-1 + A2w02 pn-2 + ... + An-1w0n-1p + w0); *
W(p) = w0n/(p2 + 2x w0 p + w02)n/2; **
W(p) = ( An-2w0n-2 p2 + An-1w0n-1p + w0n)/
/(pn + A1w0 pn-1 + A2w02 pn-2 + ... + An-1w0n-1p + w0). ***
Если все корни полинома знаменателя вещественные отрицательные разные, то переходный процесс монотонный, без перерегулирования. Наименьшее время регулирования будет, если все корни кратные. В этом случае коэффициенты А1, А2, ..., Аn-1 являются коэффициентами бинома Ньютона (р + 1)n. При x = 0,707 корни комплексные сопряжённые, переходная функция с небольшим перерегулированием и сокращается время регулирования. Если передаточная функция имеет нули, то для уменьшения выброса переходной характеристики рекомендуется распологать корни полинома знаменателя на отрицательной вещественной полуоси по арифметмческой ( если один нуль) или геометрической прогрессии (если два нуля). Приведённые в табл. 10 стандартные передаточные функции замкнутых систем обеспечивают оптимальные переходные процессы.
Таблица 10
| N | Биноминальные коэффициенты знаменателя (*) | τ |
| 1 1 1 2 1 1 3 3 1 1 4 6 4 1 | 4,8 7,9 | |
| Коэффициенты знаменателя (**) при ξ = 0,75 | ||
| 1 1,5 1 1 2,5 2,5 1 1 3 4,25 3 1 | 2,9 4,4 5,15 | |
| Коэффициенты знаменателя (***) при расположении вещественных корней по геометрической прогрессии | ||
| 1 6,7 6,7 1 1 7,9 15 7,9 1 | 1,5 3,3 | |
| Коэффициенты знаменателя (***) при расположении вещественных корней по арифметической прогрессии | ||
| 1 2,5 1 1 5,1 6,5 1 1 7,22 16,3 11,83 1 |
В более сложных случаях приравнивают коэффициенты при одинаковых степенях р числителя и знаменателя равенства и получают систему нелинейных алгебраических уравнений. Как правило, она переопределена и может быть решена методом наименьших квадратов.
Дата добавления: 2015-01-19; просмотров: 390; Мы поможем в написании вашей работы!; Нарушение авторских прав |