
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модальное управление
Сущность модального управления и его преимущества.
Поведение в системе автоматического управления определяется корнями характеристического уравнения, которым, в свою очередь, соответстуют составляющие свободного движения системы, называемые «модами».
Модальное управление — это такое управление, когда достигается требуемый характер переходных процессов за счет обеспечения необходимого расположения корней характеристического полинома на комплексной плоскости. При этом задача сводится к определению коэффициентов соответствующих обратных связей по состоянию объекта, а не путем применения корректирующих звеньев в прямой цепи САУ.
Это управление применяется тогда, когда все составляющие вектора состояния объекта управления доступны непосредственному измерению (полная управляемость).
Следует заметить, что термин “объект управления” следует воспринимать в более широком смысле, чем это принято в классической теории автоматического управления. Сюда следует относить исполнительные и рабочие органы, предшествующие им усилители и преобразователи, принимая их выходные сигналы в качестве составляющих выходного вектора объекта.
Четыре наиважнейших достоинства модального управления:
1. Синтезированная модальная САУ не требует проверки на устойчивость (так как она заранее должна быть устойчивой и обладать требуемой степенью устойчивости).
2. Синтезированная модальная САУ не требует введения дополнительных корректирующих устройств (так как она сама уже удовлетворяет требуемым показателям качества).
3. Введение модальных ОС, в силу их безынерционности, не повышает порядок объекта и не нарушает его управляемость и наблюдаемость (что зачас-
тую происходит при введении пассивных инерционных корректирующих устройств).
4. Относительная простота и экономичность технической реализации модальных САУ (так как реализации модальных ОС может быть выполнена с помощью маломощных измерительно-преобразовательных устройств и электронных усилителей с малыми тепловыми потерями).
Расчет и конструирование модальных регуляторов проводится в следующей последовательности.
Пусть полностью управляемый и наблюдаемый объект описывается следующими уравнениями в векторно-матричной форме:
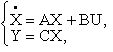
| (3.1) |
где X — n-мерный вектор переменных состояния объекта (n — порядок объекта); Y и U — векторы выходной переменной и управления; A, B и C — матрицы соответственно коэффициентов характеристического уравнения, управления и наблюдения.
Сформируем обратную связь следующим образом:
| U=K(G — LX), | (3.2) |
где G — вектор задающих сигналов; K — матрица коэффициентов усиления промежуточного регулятора (усилителя); L — матрица коэффициентов обратных связей. Тогда обобщая уравнения замкнутой системы (3.1) и (3.2) получаем:
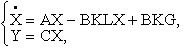
| (3.3) |
или в виде
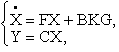
| (3.4) |
где F = A - BKL.
Характеристическое уравнение полученной замкнутой системы определяется следующим образом:
| D(p) = det|pI – F| | (3.5) |
где I — единичная матрица размерности nxn.
Поскольку собственные числа матрицы однозначно определяют коэффициенты характеристического полинома, задача может быть сформулирована следующим образом: для управляемой системы (3.1) с характеристическим полиномом 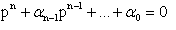 найти вектор L коэффициентов обратных связей и предварительный коэффициент усиления K, чтобы замкнутая система (3.4) имела желаемую стандартную форму характеристического полинома (3.5) с заданными коэффициентами li.
найти вектор L коэффициентов обратных связей и предварительный коэффициент усиления K, чтобы замкнутая система (3.4) имела желаемую стандартную форму характеристического полинома (3.5) с заданными коэффициентами li.
Процедура расчета коэффициентов l1,..., ln проводится в следующей последовательности:
1. Выбираем желаемое распределение корней характеристического уравнения, то есть выбираем желаемую стандартную форму характеристического полинома замкнутой системы. С целью сокращения объема вычислений для случаев объектов высокого порядка целесообразно применить описание объекта в канонической управляемой форме Фробениуса.
2. Находим характеристический полином с помощью формулы (3.5). Коэффициенты этого полинома будут зависеть от неизвестных пока параметров l1 и коэффициента усиления промежуточного усилителя K.
3. Приравниваем коэффициенты при одинаковых степенях p полиномов, полученных на первом и втором шагах, получаем систему уравнений для определения неизвестных параметров l1. Решив ее при известных остальных параметрах системы (матрицы А, B,С), находим искомые параметры модального регулятора (элементы матрицы L). При этом К промежуточного усилителя находится из условия получения требуемых переменных состояния в установившемся режиме, т.е. 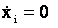 .
.
Дата добавления: 2015-01-19; просмотров: 1518; Мы поможем в написании вашей работы!; Нарушение авторских прав |