Операционный метод

Операционный метод (преобразование Лапласа) полезен как при получении модели линейной системы управления в виде передаточной функции так и при определении временных характеристик системы.

По определению преобразование Лапласа функции времени f(t) равно: ∞

F (p) = L [f(t)] = ∫ f(t) exp (- pt) dt,

⁰

где Lесть символ преобразования Лапласа. При интегрировании переменная t (время) исчезает и преобразование Лапласа представляет собой функцию комплексного переменного р. Обратное преобразование Лапласа определяется выражением

σ + j∞

f(t) = L ^–1 [F(p)] = (1 / 2πj) ∫ F(p) exp (pt) dp,

σ - j∞

где L^-1 есть символ обратного преобразования Лапласа, а j = sqrt (-1). Величина σ определяется особенностями функции F(p). Преобразования Лапласа для наиболее распространнённых функций времени сведены в таблицы, по которым в случае необходимости устанавливается соответствие между оригиналом – функцией f(t) и её изображением по Лапласу – функцией F(p).

Обычно преобразование Лапласа представляет собой отношение двух полиномов от переменной р, которое является дробно-рациональной функцией). Однако таблицы оригиналов и изображений содержат функции невысоких порядков и дробно-рациональную функцию необходимо представить в виде отдельных членов

k₁ k₂ k _n

F(p) = + + … + ,

p – p₁ p – p₂ p - p_n

которые содержаться в этой таблице. Данная процедура называется разложением на простые дроби.

Коэффициенты k_i находятся по из выражения

k_i = (p – p_i) F(p) _{P = Pi}

и называются вычетом функции F(p) в полюсе р = р_i . В общем случае вычеты функции могут быть комплексными числами.

Найдем преобразование Лапласа для экспоненты exp (- at):

∞ ∞ exp (-pt –at) ∞ 1

F(p) = ∫ exp (- at) exp (-pt) dt = ∫ exp (-at – pt) = - = .

0 0 p + a 0 p + a

Найдём обратное преобразование Лапласа для функции

5 5 k₁ k₂

F(p) = = = + .

p ² + 3p + 2 (p + 1) (p + 2) p + 1 p + 2

Вычисляем коэффициенты k₁ и k₂:

5

k ₁ = (p + 1) F(p)│_{P = - 1} = = 5;

p + 2 p = - 1

5

k ₂ = (p + 2) F(p)│_{P = - 2} = = - 5.

p + 1 p = - 2

Следовательно, исходная функция может быть представлена в виде суммы двух простых дробей

5 - 5

F(p) = + .

p + 1 p + 2

В результате обратное преобразование Лапласа принимает вид:

L^-1[F(p)] = [5 exp (-t) - 5 exp (-2t)] 1(t).

В системах более высоких порядков обычно пользуются формулами разложения Хэвисайда. Если

Х _ВЫХ (р) b₀p^m + b₁p^m-1 + …+ b_m H(p)

W (р) = = = ,

Х_ВХ (р) a₀pⁿ + a₁p^n-1 + … + a_n D(p)

корни характеристического уравнения D (p) = 0 действительные, отрицательные, разные, то

n H(p_i)

x (t) = ∑ e ^p_i ^t .

i = 1 D^´ (p_i)

H (p)

Если W (p) = и р₁ = 0 , то

p D (p)

H (0 ) n H (p_i)

x(t) = + Σ e ^p_i ^t .

D (0) i = 2 p_i D^´ (p_i)

Если имеется пара комплексных сопряжённых корней

р_{1, 2} = - α ± jω, то

H (p₁) n H (p_i )

x (t) = 2Re [ e ^p₁^t ] + ∑ e ^p_i ^t

D^´ (p₁) i = 3 D´(p_i)

Если имеется пара чисто мнимых корней p_{1, 2} = ± jω , то

H ( jω) n H (p_i)

x (t) = Im [ e ^jωt ] + ∑ e ^p_i ^t .

D´(jω) i = 3 D´(p_i)

Найдем реакцию системы управления (рис. 14.1) на входное воздей-

х_З ε 1 х

_ Тр Т = 10 с;

к_ОС = 0, 5;

а = 0, 1 с^-1.

к_ОС

Рис .14.1

ствие в виде экспрненциальной функции х_З = ехр (- а t). Находим передаточную функцию замкнутой системы

1/Tp 1 X (p)

W_З (p) = = = .

1 + к_ОС / Tp T(p + к_ОС /T) X _З (р)

Изображение входного сигнала L [f(t)] = L[ e ^{–a t} ] = 1 / (p + a).

Изображение сигнала на выходе

1 1 H (p)

X (p) = = .

T(p + к_ОС / T) p + a D (p)

Для нахождения оригинала воспользуемся формулой для случая действительных простых корней (р₁ = -к_ОС /T ; p₂ = - a.):

H (p₁) = H (p₂) = 1; D´(p) = 2p + к_ОС / T + a;

D´(p₁) = - к_ОС / T + a; D´(p₂) = к_ОС / T - a .

Следовательно,

x (t) = 2 [ exp (-0,05t) - exp (-0,1t)].

Реакция системы на экспоненциальное входное воздействие показана на рис. 14.2.

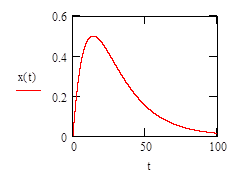Рис. 14.2