
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Третья задача кинематического анализа механизма
Относительное ускорение состоит из нормальной и тангенциальной составляющей. Нормальная составляющая относительного ускорения всегда направлена к центру вращения. Тангенциальная составляющая относительного ускорения направлена перпендикулярно звену в сторону углового ускорения.
5.1 Определяем ускорение для ведущего звена
 |
рисунок 11
 (14)
(14)
где а0 – ускорение в точке 0, м/с2
аАО – ускорение звена АО, м/с2
а0=0

 (15)
(15)
где аnАО – нормальная составляющая ускорения аАО, м/с2
аtАО – тангенциальная составляющая ускорения аАО, м/с2
так как W1=const, то аtАО=0

 (16)
(16)
W1=235.5c-1 /с.9/
LAB=0.415м /с.4/


 5.2 Определяем ускорение для группы Ассура в каждом положение
5.2 Определяем ускорение для группы Ассура в каждом положение
 |
Рисунок 12
 (17)
(17)
где аВАх – ускорение звена ВА, м/с2
 (18)
(18)
 (19)
(19)
где аnBA – нормальная составляющая ускорения аBA, м/с2
аtBA – тангенциальная составляющая ускорения аBA, м/с2
 (20)
(20)
где W2х – угловая скорость шатуна, с-1 /с.13, табл.2/
LAB=1.885м
Числовые значения приведены в таблице 3
Таблица 3
| W2, с-1 | 37.1 | 37.1 | 51.8 | 37.1 | 37.1 | 51.8 | ||
| аnBA, м/с |
5.3 Определяем масштаб плана ускорения

 (21)
(21)
где а’А – отрезок ускорения ведущего звена на плане ускорения в 1, 3, 5, 7 положениях мм
а’А=115,08мм
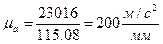
5.4 Определяем размер отрезка нормальной составляющей ускорения аnВА в 1, 3, 5, 7, положениях на плане ускорения
 (22)
(22)
где аnВА=2596м/с2 /с.15, табл.3/

5.5 Определяем размер отрезка нормальной составляющей ускорения аnВА в 4,8 положениях на плане ускорения
аnВА=5058м/с2

Отрезок аnВА во 2 и 6 положениях равен нулю.
Строим восемь планов ускорения.
Принцип построения плана ускорений такой же, как и у плана скоростей.
На ватмане берем любую точку (полюс). В начале переносим параллельно (в заданном положении механизма) вектор аА через эту точку. Откладываем его длину в масштабе от полюса. В конец вектора аА параллельно переносим вектор аnВА. Откладываем его длину в масштабе от конца вектора аА (Рисунок 13).

 |
Рисунок 13
В конец вектора аnВА переносим параллельно вектор аtВА, но направление мы не знаем. Поэтому проводим этот вектор в обе стороны относительно конца вектора аnВА. В полюсную точку переносим параллельно вектор аВ, но направление его мы также не знаем. Поэтому проводим этот вектор в обе стороны относительно полюса. Пересечение векторов аnВА и аВ дадут нам их длины. Указываем направление аnВА и аВ согласно уравнению. Для нахождения ускорения средней точки Шатуна S2 нужно соединить точки a и b прямой линией и направить вектор ускорения из полюса к середине прямой ab. (рисунок 14).
Отрезок аnВА во 2 и 6 положениях равен нулю. Следовательно вектор аtВА будет выходить из конца вектора аА.
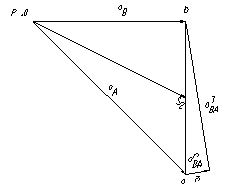 |
Рисунок 14
5.6 Определяем тангенциальное ускорение шатуна в каждом положении
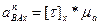 (23)
(23)
где [t] – длина отрезка t для х – положения
m=200м/с2/мм /с.16/
 5.7 Определяем ускорения ползуна в каждом положении
5.7 Определяем ускорения ползуна в каждом положении
 (24)
(24)
[P,b]x – длина отрезка Pb для х – положения
5.8 Определяем ускорение в точке S2
 (25)
(25)
[P, S2]х – длина отрезка [P, S2] в х – положении
Числовые значения ускорений приведены в таблице 4
Таблица 4
| № положения | [t], мм | аtBA м/с2 | [P,b], мм | аBA, м/с2 | [P,S2]мм | aS2 м/с2 |
| 80,33 | 81,69 | 91,12 | ||||
| 117,97 | 25,97 | 58,99 | ||||
| 80,33 | 81,05 | 90,74 | ||||
| 89,79 | 102,3 | |||||
| 80,33 | 81,05 | 90,74 | ||||
| 117,97 | 25,97 | 58,99 | ||||
| 80,33 | 81,69 | 91,12 | ||||
| 89,79 | 102,3 |
5.9 Определяем угловые ускорения для каждого положения
 (26)
(26)
аtВАх –тангенциальная составляющая ускорения в х –положении, м/с2 /табл.4/
LAB=1,885м /с.4/
Числовые значения углового ускорения приведены в таблице 5
таблице 5
| аtВА м/с2 | ||||||||
| e, с-2 |
Дата добавления: 2015-01-19; просмотров: 409; Мы поможем в написании вашей работы!; Нарушение авторских прав |