
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рычаг Жуковского
9.1 Строим схему нагрузки сил на механизм в заданном положении для расчета
Момент инерции заменяем парой сил.
Надо обращать внимание на верность направление этих сил.
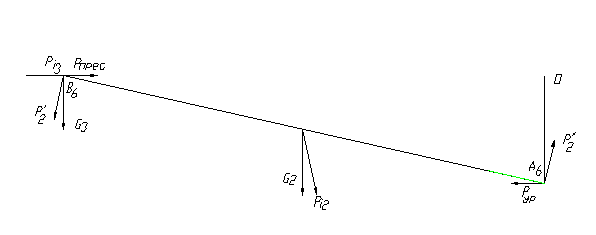 |
Рисунок 29
9.2 Построения сил на плане скорости
Берем план скорости для заданного положения механизма для расчета и поворачиваем его на 900. Теперь все силы параллельно самим себе переносим со схемы нагрузки сил на механизм в соответствующие точки (a и b) плана скоростей (Рисунок 30) .
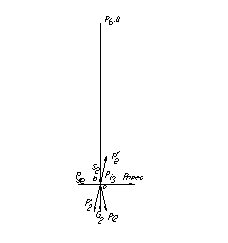
Рисунок 30
9.3 Составляем векторное уравнение


где hi2 – плече силы Pi2 относительно полюса, мм
Р’2 и P”2 – пары сил, Н
h”2 и h’2 –плечи пары сил, мм
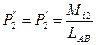
где Mi2=15621232Hм /с.25/
LAB=1.885м /с. 4/

h”2=h’2=21,3мм
[Ра]=97,72мм
hi2=21,5мм
Pi2=16582089H /с.25/
Рпресс=320000Н /с. 4/
Pi3=12166945H /с. 25/
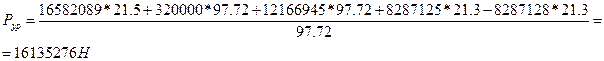
9.4 Сравнение результатов
Полученный результат уравновешенной силы полученный методом рычага Жуковского сравниваем с полученным результатом уравновешенной сила при расчете ведущего звена. Разница этих данных не должна превышать 5%.
 (52)
(52)
где РЖур – уравновешающия сила полученная методом рычага Жуковского, Н
РВЗур – уровновешающия сила полученная при расчете ведущего звена, Н
РВЗур=16136019Н /с. 32/

 10 Определение передаточных чисел четырех типовых планетарных редукторов
10 Определение передаточных чисел четырех типовых планетарных редукторов
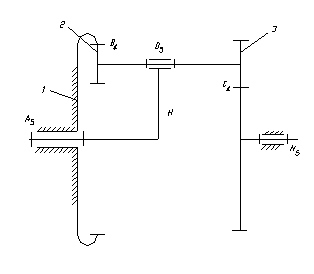
10.1 Определение передаточного числа планетарного редукторов с двумя внешними зацеплениями
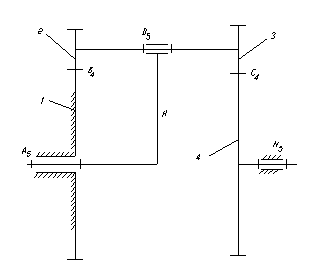 |
Рисунок 31
1 – неподвижное звено;
2, 3 – блок сателлитов;
4 – подвижное колесо;
Н – водило;
А5 - кинематическая пара пятого класса, низшая;
D5 - кинематическая пара пятого класса, низшая;
N5 - кинематическая пара пятого класса, низшая;
С4 - кинематическая пара четвертого класса, высшая;
В4 - кинематическая пара четвертого класса, высшая;
10.1.1 Определяем степень подвижности
 (53)
(53)
где n=3
р5=3
р4=2

Если степень подвижности равна единицы, то данный редуктор является планетарным.
10.1.2 Определяем передаточное отношение от подвижного колеса к водилу
Верхний индекс показывает, какое звено неподвижно.
 Мысленно остановить водило, и заменить неподвижное колесо подвижным. Теперь следует определять от подвижного колеса к тому колесу, которое было неподвижным. Полученный результат нужно вычесть из единицы.
Мысленно остановить водило, и заменить неподвижное колесо подвижным. Теперь следует определять от подвижного колеса к тому колесу, которое было неподвижным. Полученный результат нужно вычесть из единицы.
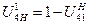 (54)
(54)
где m – число внешних зацеплений;
UH41 – передаточное отношение от 4 к 1 колесу
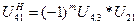 (55)
(55)
где U4.3 – передаточное отношение от 4 к 3 колесу
U21 – передаточное отношение от 2 к 1 колесу
m=2
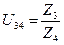 (56)
(56)
где Z3 – число зубьев третьего сателлита;
Z4 – число зубьев подвижного колеса 4;
Z3=19
Z4=45
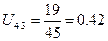
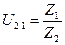 (57)
(57)
где Z1 – число зубьев неподвижного колеса 1;
Z4 – число зубьев подвижного колеса 4;
Z1=47
Z2=18
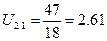



10.1.3 Определяем передаточное отношение от водила к подвижному колесу
Искомое передаточное отношение обратное передаточному отношению от подвижного колеса к водилу. Следовательно, нужно 1 поделить на передаточное отношение от подвижного колеса к водилу.
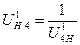 (58)
(58)
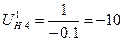
 |
10.2 Определение передаточного числа планетарного редуктора с одним внешними и одним внутренним зацеплениями
Рисунок 32
1 – неподвижное звено;
2, 3 – блок сотилитов;
4 – подвижное колесо;
Н – водило;
А5 - кинематическая пара пятого класса, низшая;
D5 - кинематическая пара пятого класса, низшая;
N5 - кинематическая пара пятого класса, низшая;
С4 - кинематическая пара пятого класса, высшая;
В4 - кинематическая пара пятого класса, высшая;
10.2.1 Определяем степень подвижности
 |

где n=3
р5=3
р4=2

10.2.2 Определяем передаточное отношение от подвижного колеса к водилу
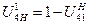 (59)
(59)
где m – число внешних зацеплений;
UH41 – передаточное отношение от 4 к 1 колесу
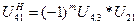 (60)
(60)
где U4.3 – передаточное отношение от 4 к 3 колесу
U21 – передаточное отношение от 2 к 1 колесу
m=1
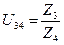 (61)
(61)
где Z3 – число зубьев третьего сателлита;
Z4 – число зубьев подвижного колеса 4;
Z3=19
Z4=45
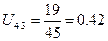
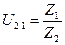 (62)
(62)
где Z1 – число зубьев неподвижного колеса 1;
Z4 – число зубьев подвижного колеса 4;
Z1=47
Z2=18




10.2.2 Определяем передаточное отношение от водила к подвижному колесу
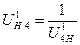 (63)
(63)

10.3 Определение передаточного числа планетарного редукторов с двумя внутренним зацеплениями
 |
Рисунок 33
1 – неподвижное звено;
2, 3 – блок сателлитов;
4 – подвижное колесо;
Н – водило;
А5 - кинематическая пара пятого класса, низшая;
D5 - кинематическая пара пятого класса, низшая;
N5 - кинематическая пара пятого класса, низшая;
С4 - кинематическая пара четвертого класса, высшая;
В4 - кинематическая пара четвертого класса, высшая;
10.3.1 Определяем степень подвижности

где n=3
р5=3
р4=2

10.3.2 Определяем передаточное отношение от подвижного колеса к водилу
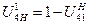 (64)
(64)
где m – число внешних зацеплений;
UH41 – передаточное отношение от 4 к 1 колесу
 |
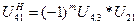 (65)
(65)
где U4.3 – передаточное отношение от 4 к 3 колесу
U21 – передаточное отношение от 2 к 1 колесу
m=0
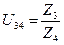 (66)
(66)
где Z3 – число зубьев третьего сателлита;
Z4 – число зубьев подвижного колеса 4;
Z3=18
Z4=59

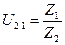 (67)
(67)
где Z1 – число зубьев неподвижного колеса 1;
Z4 – число зубьев подвижного колеса 4;
Z1=60
Z2=19
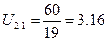

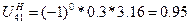

10.3.3 Определяем передаточное отношение от водила к подвижному колесу
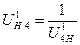 (68)
(68)
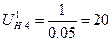
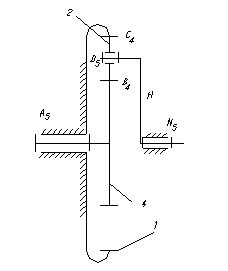 |
10.4 Определение передаточного числа планетарного редукторов с внутренним зацеплением и паразитным колесом
1 – неподвижное звено;
2 – сателлит;
4 – подвижное колесо;
Н – водило;
А5 - кинематическая пара пятого класса, низшая;
D5 - кинематическая пара пятого класса, низшая;
N5 - кинематическая пара пятого класса, низшая;
С4 - кинематическая пара четвертого класса, высшая;
В4 - кинематическая пара четвертого класса, высшая;
10.4.1 Определяем степень подвижности

 |
где n=3
р5=3
р4=2

10.4.2 Определяем передаточное отношение от подвижного колеса к водилу
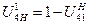 (69)
(69)
где m – число внешних зацеплений;
UH41 – передаточное отношение от 4 к 1 колесу
 (70)
(70)
где U4.2 – передаточное отношение от 4 ко 2 колесу
U21 – передаточное отношение от 2 к 1 колесу
m=1
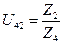 (71)
(71)
где Z2 – число зубьев сателлита;
Z4 – число зубьев подвижного колеса 4;
Z2=20
Z4=25
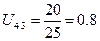
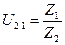 (72)
(72)
где Z1 – число зубьев неподвижного колеса 1;
Z4 – число зубьев подвижного колеса 4;
Z1=65
Z2=20
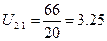
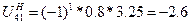

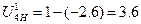
10.4.3 Определяем передаточное отношение от водила к подвижному колесу
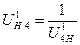 (73)
(73)

Дата добавления: 2015-01-19; просмотров: 425; Мы поможем в написании вашей работы!; Нарушение авторских прав |