
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Nbsp; 7 Определение реакций опор для группы Ассура
Рисунок 21 – действие сил в заданном положение механизма для расчета
Для построения всех сил нужно знать что:
- силы инерции Рi всегда направлены в противоположную сторону ускорению центра масс звена;
- момент инерции направлен в противоположную сторону угловому ускорению звена, для заданного положения механизма;
- сила прессования направлена в противоположную сторону рабочему ходу механизма;
- силы тяжести направлены вниз;
- сила R03 ,с которой действует стойка на ползун направлена вверх;
- направления тангенциальной и нормальной составляющей силы с которой действует кривошип на шатун, мы не знаем, поэтому первоначально их направляем в любом направлении.
7.1Определяем силу тяжести шатуна
 (32)
(32)
где m2 – масса шатуна, кг
q – ускорение свободного падения, м/с2
m2=1405.5кг /с.2/
q=9,81 м/с2

7.2 Определяем силу тяжести ползуна
 (33)
(33)
где m3 – масса ползуна, кг
m3=2342,5кг /с.2/


7.3 Определяем силу инерции шатуна
 (34)
(34)
где аS6 – ускорение относительно центра масс шатуна в шестом положении
аS6= 11798 м/с2 /с.18, табл.4/


7.4 Определяем силу инерции ползуна
 (35)
(35)
где аВ6 – ускорение относительно центра масс ползуна в шестом положении
аВ6= 5194 м/с2 /с.18, табл.20/

7.5 Определяем момент инерции пары сил
 (36)
(36)
где e - угловое ускорение, рад/с2
JS – момент инерции шатуна относительно оси, проходящей через центр тяжести
 (37)
(37)
LAB=1,885м /с.4/
m2=1405.5кг /с.2/

e2=12512 /с.18, табл.18/

7.6 Найдем сумму всех сил относительно точки В
 (38)
(38)
 где RТ12 –тангенциальная составляющая реакции, с которой действует кривошип на шатун, Н
где RТ12 –тангенциальная составляющая реакции, с которой действует кривошип на шатун, Н
h2 – плечо силы тяжести относительно точки В, мм
hi2 - плечо силы инерции относительно точки В,мм
G2=13788 H
h2=91,2мм
hi2=84,47 мм
mе=0,01м/мм /с. 5/
Pi2=16582089H /с. 25/
AB=185.5 мм /с. 4/
 (39)
(39)

Получилось выражение со знаком «-», следовательно нужно изменить направление вектора RТ12 на противоположное.
7.7 Составим векторное уравнение
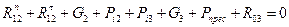 (40)
(40)
где Rn12 – нормальная составляющая силы, с которой действует кривошип на шатун, Н
Рпрес – сила прессования механизма, Н
R03 – сила с которой действует стойка на ползун, Н
RT12=1601767H
G2=13788 H
Pi2=16582089H /с. 25/
Pi3=12166945H /с. 25/
G3=22980H /с.25/
Pпрес=320000Н /с. 2/
7.8 Выбираем масштаб

7.9 Определяем на графике длины всех сил
 (41)
(41)
 |
где Zx – действующая сила
mR=110000Н/мм /с. 26/
Численные значения длин векторов сил на графике приведены в таблице 6
Таблица 6
| Zx | RT12 | G2 | Pi2 | Pi3 | G3 | Pпрес |
| Значение, Н | ||||||
| N, мм | 0,13 | 165,8 | 121,6 | 0,2 | 3,2 |
Строим график данного векторного уравнения и найдем R03 и Rn12
На ватмане бумаги берем произвольную точку. В эту точку с заданного положения механизма для расчета переносим вектор силы RT12 в масштабе. Так как у нас векторное уравнение то остальные вектора сил переносятся так же параллельно в конец предыдущего вектора(рисунок 22).
Для нахождения вектора Rn12 параллельно переносим его в начальную точку и проводим до пересечения с вектором R03. Расставляем их направления (рисунок 23).
Для нахождения силы R12 надо направит вектор от начала вектора Rn12 к концу вектора Rn12.(рисунок 23)

Рисунок 22
 |

Рисунок 23
7.10 Определяем силу, с которой действует кривошип на группу Ассура
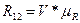 (42)
(42)
где V – длина вектора R12 на графике, мм
V=162,14 мм /с. 27, табл.6/
mR=100000 Н/мм /с. 26/

Дата добавления: 2015-01-19; просмотров: 434; Мы поможем в написании вашей работы!; Нарушение авторских прав |