
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Максимум пайда табу
Есеп жалпы түрде шығарылатын болғандықтан параметрлерді анықтау үшін шартты белгілеулер енгіземіз.
n - өнім түрлері
m – шикізат түрлері
bi - і-ші шикізат мөлшері і=1,m
aij - j – ші өнімнің бір данасына кететін і-ші шикізаттың мөлшері
Cj – j – ші өнімнің бір данасынан түсетін пайда.
Басқарушы немесе негізгі айнымалы
Хj – j – ші өнімнің көлемі
Есептің шектеуі, шикізат бойынша шектеу және басқарушы айнымалылар, теріс емес шарты.
Есепті шешу нәтижесінде бір өндірістің жағадайына сәйкес максималда пайда беретін өндірістің шамасын табуымыз керек. Ол үшін табылатын өнім шамасын хj деп белгілейміз. Онда барлық өнім түрлерін сатудан түсетін пайданың жиынтығы мына өрнекпен сипатталады:
F=C1x1+C2x2+...+Cnxn→max
Бірақ өнім өндіруге і – түрлі ресурстың шығыны қолда бардан аспауға тиісті:
a11x1+a12x2+...+a1nxn ≤ b1
a21x1+a22x2+...+a2nxn ≤ b2
........................................
am1x1+am2x2+...+amixn ≤ bm
xj ≥0 j=1,n 1
Табылатын мәндердің экономикалық мағынасы болу үшін, олар теріс сан болмауға тиісті : хj ≥ 0, j = .
Келтірілген теңсіздіктер есептің шектеулер жүйесін құрастырады. Есептің математикалық түрін қысқаша былай жасауға болады:
Z= →max
≤ , i = .
хj ≥ 0, j = .
Математикалық тұрғыда есептің шешуі нәтижесінде сызықтық функцияны максималға жеткізетін белгісіз х1....хn мәндердің шамаларын табу керек.
4. Диета есебінің математикалық моделі
Имеется два вида корма I и II, содержащие питательные вещества (витамины)  ,
,  и
и  . Содержание количества единиц питательного вещества в 1 кг каждого вида корма и стоимость 1 кг корма приведены в таблице 10.2.
. Содержание количества единиц питательного вещества в 1 кг каждого вида корма и стоимость 1 кг корма приведены в таблице 10.2.
Таблица 10.2
| Питательные вещества | Необходимый минимум питательных веществ | Количество единиц питательного вещества в 1 кг корма | |
| Корм I | Корм II | ||

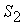

| 
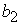

| 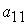

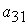
| 


|
| Стоимость 1 кг корма (в руб.) | 
| 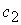
|
Необходимо составить дневной рацион, в котором содержание каждого вида питательных веществ было бы не менее установленного минимума, причем затраты на него должны быть минимальными.
Составим экономико-математическую модель задачи. Обозначим через 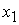 и
и  соответственно количество кормов I и II, входящих в дневной рацион. Принимая во внимание значения, приведенные в табл. 10.2, и условие, что дневной рацион удовлетворяет требуемой питательности только в случае, если количество единиц питательных веществ не меньше предусмотренного, получим систему ограничений
соответственно количество кормов I и II, входящих в дневной рацион. Принимая во внимание значения, приведенные в табл. 10.2, и условие, что дневной рацион удовлетворяет требуемой питательности только в случае, если количество единиц питательных веществ не меньше предусмотренного, получим систему ограничений
 (10.4)
(10.4)
Кроме того, переменные
 ,
,  . (10.5)
. (10.5)
Общая стоимость рациона (в руб.) составит
 . (10.6)
. (10.6)
Итак, экономико-математическая модель задачи: составить дневной рацион  , удовлетворяющий системе (10.4) и условию (10.5), при котором функция (10.6) принимает минимальное значение.
, удовлетворяющий системе (10.4) и условию (10.5), при котором функция (10.6) принимает минимальное значение.
5. Тиімді пішу есебінің математикалық моделі
Для изготовления двух видов продукции  и
и  используют три вида сырья:
используют три вида сырья:  ,
, 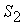 и
и  . Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 10.1. Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 10.1. Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
Таблица 10.1
| Виды сырья | Запасы сырья | Количество единиц сырья, затрачиваемых на изготовление единицы продукции | |

| 
| ||

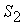

| 
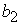

| 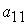

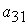
| 


|
| Прибыль от единицы продукции (в руб.) | 
| 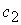
|
Составим экономико-математическую модель (математическое описание исследуемого экономического процесса) задачи.
Обозначим через 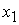 ,
,  количество единиц продукции соответственно
количество единиц продукции соответственно  ,
,  , запланированных к производству. Тогда учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений
, запланированных к производству. Тогда учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений
 (10.1)
(10.1)
По смыслу задачи переменные  ,
,  . (10.2)
. (10.2)
Суммарная прибыль F(x) составит  руб. от реализации продукции
руб. от реализации продукции  и
и  руб. – от реализации продукции
руб. – от реализации продукции  , т.е.
, т.е.
 . (10.3)
. (10.3)
Итак, экономико-математическая модель задачи: найти такой план выпуска продукции  , удовлетворяющий системе (10.1) и условию (10.2), при котором функция (10.3) принимает максимальное значение.
, удовлетворяющий системе (10.1) и условию (10.2), при котором функция (10.3) принимает максимальное значение.
Задачу легко обобщить на случай выпуска n видов продукции с использованием m видов сырья.
6. Сызықтық программалау есебінің түрлері
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
 (8)
(8)
при условиях
 (9)
(9)
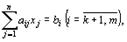 (10)
(10)
 (11)
(11)
где 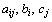 - заданные постоянные величины и
- заданные постоянные величины и  .
.
Дата добавления: 2015-01-19; просмотров: 274; Мы поможем в написании вашей работы!; Нарушение авторских прав |