СП есебіндегі мүмкін болатын шешімдер жиыны және оптимал шешім

Тиімді шешім табу (ең үлкен немесе ең кіші шешім) мәселесімен ерте заманнан бастап кӛптеген оқымысты ғалымдар айналысты, сонымен қатар олар табылған әдістерді әртүрлі ғылым салаларында, оның ішінде: математикада, механикада, физикада т. б. ілімдерде қолдана білді. Қандай есепті құрастырмасақ та, тиімді шешім табу үшін алдымен алдымызға мақсат қою қажет, ал мақсатты функция берілген жағдайды немесе шарттарды қанағаттандыруы керек. Мақсатты функцияға және шарттарға енген белгісіздер ӛте кӛп және үлкен дәрежелі болуы мүмкін. Егер есепке енген белгісіздердің дәреже кӛрсеткіші бірден артпаса, онда мұндай есептерді сызықты алгебра есептеріне жатқызады. Мұндай жағдайда есептің берілген шарттары сызықты теңдеу немесе теңсіздіктер түрінде беріледі.

Сызықтық бағдарламалау есебі былай анықталады.

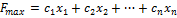,функцияның кризистік мәні келесі шектеулерді қанағаттандыратын

есеп сызықтық бағдарламалаудың жалпы есебі деп аталады. жүйесі шектеулер жүйесі деп аталады, ал (1.1) сызықтық функция -

мақсатты функция.

Теорема 1.1.(тірек жоспарының оптималдылық белгісі). Егер кез келген j үшін болса, (1)-(3) есептердің тірек жоспары оптималды болып табылады.

Теорема 1.2. Егер қандай да бір j=k үшін 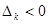және 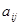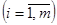сандар ішінде оң сан жоқ болса, онда (1)-(3) есептердің (1) мақсат функциясы оның жоспарларының жиынымен шектелмеген.

Теорема 1.3.Егер (1)-(3) есептердің Х тірек жоспары көрсетілмесе және 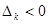болса, бірақ сандарының ішінде оң сандар бар болса, онда сияқты Х¹ тірек жоспары бар болады.

Жоғарыдағы теоремалар табылған тірек жоспары оптималды болатынын тексеруге мүмкіндік береді және жаңа тірек жоспарға ауысуды мақсатқа лайықты көрсету.