
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
МНОГОЭТАПНЫЕ ПРОИЗВОДСТВЕННО-ТРАНСПОРТНЫЕ ЗАДАЧИ
Многоэтапными производственно-транспортными задачами будем называть такие, которые отображают последовательные процессы выпуска одного вида продукции, доставки его в пункты переработки в другую продукцию, производства этой продукции и доставки ее конечным потребителям. В самых простых постановках таких задач рассматриваются два продукта – “сырье” и “готовый продукт”. Возможно и большее число наименований: “сырье”, “полуфабрикат”, “готовый продукт”. При определенных условиях и такие, формально многопродуктовые задачи, могут быть сведены к однопродуктовым задачам шахматного типа. Главное из этих условий – одинаковые нормы расхода одной продукции на производство другой во всех пунктах переработки.
Формальная постановка самой простой многоэтапной задачи:
10. 
11. 
12. 
13. 
14. 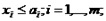
15. 
16. 
17. 
Обозначения: xi – искомый объем добычи сырья в пункте i; yj – искомый объем производства готовой продукции в пункте j; xij – искомый объем перевозок сырья из пункта i в пункт j; yjk – искомый объем перевозки готовой продукции из пункта j в пункт k; ai – максимально возможный объем добычи сырья в пункте i; qj – максимально возможный объем выпуска готовой продукции в пункте j; g – расход сырья на единицу готовой продукции; ci – удельные затраты на добычу сырья в пункте i; tj - удельные затраты на производство готовой продукции в пункте j; sij - удельные затраты на перевозку сырья из пункта i в пункт j; pjk – удельные затраты на перевозку готовой продукции из пункта j в пункт k; bk – спрос на готовую продукцию в пункте k.
Целевой функцией является минимизация всех суммарных затрат на производство и транспортировку сырья и готовой продукции.
Модель 10. – 17. нельзя свести к математической транспортной задаче лишь путем изменения знаков в ограничениях 14. и 15.
Во-первых, среди коэффициентов матрицы A есть не только нули и единицы,
во-вторых, некоторые переменные (yj) встречаются в ограничениях не два, а три раза.
Первую проблему легко решить путем замены переменных: gyj =  . Экономически это соответствует переходу к новой единице измерения готовой продукции – количеству сырья, пошедшему на ее изготовление (аналогичный прием используется иногда и в реальности, например, объем производства цельномолочной продукции в промышленности – молока разных видов, сливок, сметаны, кефира и т.п. – измеряется количеством молока определенной жирности, пошедшего на изготовление разнообразных молочных продуктов).
. Экономически это соответствует переходу к новой единице измерения готовой продукции – количеству сырья, пошедшему на ее изготовление (аналогичный прием используется иногда и в реальности, например, объем производства цельномолочной продукции в промышленности – молока разных видов, сливок, сметаны, кефира и т.п. – измеряется количеством молока определенной жирности, пошедшего на изготовление разнообразных молочных продуктов).
После замены переменных в ограничениях 11. уже нет коэффициентов, отличных от нуля и единицы. Далее аналогичный переход к новым единицам измерения осуществляется в ограничениях 12., 13. и 15. – их правые и левые части умножаются на g, после чего вместо прежних переменных и параметров вводятся новые: gyjk =  ; gbk =
; gbk =  ; gqj =
; gqj =  . В целевой функции в связи с заменой переменных также происходит замена параметров:
. В целевой функции в связи с заменой переменных также происходит замена параметров:  .
. 
После замены переменных и параметров модель 10. – 17. будет иметь следующий вид:
10а. 
11а. 
12а. 
13а. 
14а. 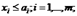
15а. 
16а. 
17а. 
В полученной задаче остается один “дефект” – переменные 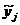 встречаются не в двух, а в трех ограничениях. Его легко устранить, если доказать, что ограничения 11а. на оптимальном плане выполняются как равенства (это легко сделать от противного), использовать эти равенства для выражения
встречаются не в двух, а в трех ограничениях. Его легко устранить, если доказать, что ограничения 11а. на оптимальном плане выполняются как равенства (это легко сделать от противного), использовать эти равенства для выражения 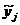 через суммы xij, и осуществить подстановку в ограничения 12а. В ограничениях 14а. и 15а. изменим знаки на противоположные и получим задачу, удовлетворяющую определению математической транспортной задачи. Но это будет задача в сетевой постановке, и для перехода к задаче шахматного типа необходимо будет избавиться от переменных xi и
через суммы xij, и осуществить подстановку в ограничения 12а. В ограничениях 14а. и 15а. изменим знаки на противоположные и получим задачу, удовлетворяющую определению математической транспортной задачи. Но это будет задача в сетевой постановке, и для перехода к задаче шахматного типа необходимо будет избавиться от переменных xi и 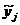 .
.
Легко доказать от противного, что при положительных параметрах затрат ограничения 10а., 11а., 12а, 13а. на оптимальном плане выполняются как равенства. Первые три из них можно использовать для замены переменных и подстановки в другие ограничения. Выразим xi через суммы объемов вывоза и эти выражения подставим в ограничения 14а. Выразим 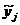 через суммы объемов ввоза и подставим в ограничения 15а. Одновременно справедливым должно быть ограничение, полученное путем подстановки в 15а. выражений
через суммы объемов ввоза и подставим в ограничения 15а. Одновременно справедливым должно быть ограничение, полученное путем подстановки в 15а. выражений 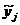 через суммы объемов вывоза, полученных из 12а. В результате всех подстановок получим следующую совокупность ограничений:
через суммы объемов вывоза, полученных из 12а. В результате всех подстановок получим следующую совокупность ограничений:




Сводим последние три группы ограничений к равенствам путем введения дополнительных переменных, причем в последние две группы неравенств не потребуются разные дополнительные переменные, поскольку правые части у них совпадают, и нам известно также, что  . Обозначим эти переменные как zjj , получим следующую систему равенств:
. Обозначим эти переменные как zjj , получим следующую систему равенств:


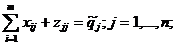

Для удобства ограничения переставлены местами. Первые две группы ограничений являются строчными (изменяется второй индекс, распределяется по потребителям произведенная продукция), вторые две группы – столбцовыми (изменяется первый индекс, складываются объемы поставок от разных производителей). В этой задаче две группы производителей – производители сырья и производители готовой продукции, а также две группы потребителей – потребители сырья и потребители готовой продукции. Достаточное и необходимое условие разрешимости такой задачи – выполнение одновременно двух условий:
 и
и  .
.
После подстановок использованных выражений переменных в целевую функцию она приобретет следующий вид:

При всех дополнительных переменных коэффициенты нулевые.
33. Экономическая постановка производственно-транспортной задачи.
Во второй серии расчетов формировались и решались задачи оптимизации использования специализированных ремонтных производств по одному отдельному виду подвижного состава (по тепловозам, в разрезе различных серий), с учетом (оптимизации) затрат на прикрепление поставщиков ремонтируемого подвижного состава (железных дорог - "потребителей" услуг по ремонту подвижного состава).
Таким образом, целью этой серии расчетов является определение такого распределения объемов ремонта тепловозов по ремонтным предприятиям (при ограниченных возможностях по объемам ремонта и заданной специализации), которое может сложиться при достижении минимальных текущих затрат, с учетом оптимального прикрепления "поставщиков" ремонтируемого подвижного состава.
В этих задачах подвижной состав представляется в агрегированном виде, а все виды ремонтов сведены в один. Текущие затраты (себестоимость) на производство ремонта агрегированной единицы подвижного состава взяты из соответствующей "Справки о стоимости единицы подвижного состава при КР1 и КР2" и, из-за отсутствия необходимой информации, при расчетах " заказа" использовались затраты на КР1.
В качестве затрат, связанных с поставкой тепловозов от дороги потребителя до ремонтного завода, рассматривались величины пропорциональные расстояниям между ними (одна группа вариантов) или линейно связанные с этим расстоянием. Эти величины нами рассматривались как оценки "транзакционных" затрат, связанных с передачей ремонтируемого подвижного состава на соответствующий завод.
Введем обозначения:
tijp - "транзакционные" издержки на передачу тепловозов i- го вида j-ой железной дороги для ремонта на p-ом ремонтном заводе;
Ljp - расстояние между "центром" j-ой железной дороги и p-ым ремонтным заводом;
Далее мы предполагали, что "транзакционные" издержки линейно зависят от расстояния и не зависят от серии тепловоза, то есть выполняется соотношение:
tijp = H Ljp +G,
где H и G - константы. Никакой дополнительной информации по значению этих величин мы не имели, поэтому использовались экспертные оценки. В предположении, что "транзакционные" издержки составляют около десяти процентов средней себестоимости ремонта и не зависят от серии ремонтируемых тепловозов, нами были проведены серии расчетов исходя из следующих значений этих параметров:
а) H = 16.0; G = 0
б) H = 10.0; G = 5000
Естественно, это очень грубая прикидка и нами она использовалась лишь для оценки поведения решения по модели при разных гипотезах относительно "транзакционных" издержек. Отметим, что если этими затратами можно пренебречь, то задача сводится к производственной, которая рассматривалась в предыдущей серии расчетов.
Вся необходимая информация приведена ниже:
Текущие затраты по ремонту тепловозов
| Тепловозы | Астра-ханский ТРЗ | Воро-нежский ТРЗ | Мичу-ринский ЛРЗ | Орен-бургский ЛРЗ | Уфим-ский ТРЗ | Уссурий-ский ЛРЗ |
| 2ТЭ116 | ||||||
| ТЭ10в/и | ||||||
| М62 | ||||||
| ТЭП60 | ||||||
| ТЭП70 | ||||||
| ЧМЭЗв/и | ||||||
| ТЭМ2 | ||||||
| ТЭ3(ТЭМ7) | ||||||
| Астра-ханский ТРЗ | Воро-нежский ТРЗ | Мичу-ринский ЛРЗ | Орен-бургский ЛРЗ | Уфим-ский ТРЗ | Уссурий-ский ЛРЗ | |
| Проектная мощность | ||||||
| "Фактическая" |
Дата добавления: 2015-01-19; просмотров: 372; Мы поможем в написании вашей работы!; Нарушение авторских прав |