КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графиктік және симплекс әдістері бойынша есептің шешімі болмайтын жағдайды анықтау
Симплекс-метод был разработан и впервые применен для решения задач в 1947 г. американским математиком Дж. Данцигом.
Симплексный метод в отличие от геометрического универсален. С его помощью можно решить любую задачу линейного программирования.
В основу симплексного метода положена идея последовательного улучшения получаемого решения.
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (или, по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение - вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).
Таким образом, имея систему ограничений, приведенную к канонической форме (все функциональные ограничения имеют вид равенств), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении целевая функция, если и не достигнет оптимума, то приблизится к нему (или, по крайней мере, не удалится от него).
14. Сызықты программалау есебін шешудің графиктік әдісі
Сызықты программалаудың есептерінің мүмкін болатын шешімдер жиыны дөңес көпбұрышты (немесе дөңес көпбұрыш облысын) құрайды, ал есептің оптималды шешімі шешімдер көпбұрышының 1 бұрыштық нүктесінде болады. Екі белгісізі бар сызықты программалаудың стандартты есебінің мысалын қарастырайық.
Сызықтық программалау есебін графиктік әдіспен шешудің алгоритмі
1. Түзулердің графигін салу. Түзулердің теңдеуі шектеулік белгісін тура теңдік белгісіне ауыстыру арқылы алынады.
Сызықты программалаудың оптималды шешімі дөңес беттің шегінде болады.
2. Есептің шектеулер жүйесінен анықталатын жарты жазықтықты табу.
3. Шешімдердің көпбұрышын табу керек.
4. Мүмкін болатын шешімдердің векторы
табу.
5. Шешімдер көпбұрышы арқылы өтетін 
( 
- кез келген сан), түзуін салу.
6. түзуін 
бағытымен перпендикуляр вектор бағытында жылжыту керек. Нәтижесінде мақсатты функция не максимум немесе мимнимум мәнге жететін нүктелерді, не шексіздікке жететінін анықтау.
7. Функция максимумының координат нүктелерін анықтап, мақсатты функцияның сол нүктедегі мәнән есептеу.
15. Симплекс әдісі алгоритмі
1. Алғашқы тіреуіш жоспарын анықтайды.
2. Симплекс кестесін құрайды.
3. Соңғы m+1- і жолдағы 
-дің мәндерін анықтаймыз. Егер барлық 
болса,онда тіреуіш жоспары ең қолайлы болғаны. Егер -дің ішінде теріс мәндер болса,есептің шешімінің жоқтығы немесе келесі жаңатіреуіш жоспарына көшу мүмкіндігі анықталады.
4. Бағыттауыш бағана мен жол анықталады. Бағыттауыш бағана мына шартmax 
бойынша анықталады, ал бағыттауыш жол В векторыныңкомпоненттердің бағыттауыш бағананың оң компоненттеріне қатынастарының минимумы бойынша анықталады.
5. Жаңа кестені оның оптимальдық шартын тексереміз. Егер жоспар қолайлыболмаса, онда 4-кезеңге, ал жоспар қолайлы (оптимальды) болса немесе есептің шешімі жоқ болса, онда процесс аяқталады деп есептейміз.
16. Сиплекс әдісі бойынша жоспардың оптимал болу критериі
Сонымен, симплекс әдісімен оптималды жоспарды табу келесі этаптардан тұрады:
1. Тірек жоспарды табады.
2. Симплексм-кесте құрады.
3. Бір теріс сан 
бар болуын анықтайды. Егер болмаса, табылған тірек жоспар оптималды. Егер сандар ішінде терісі бар болса, онда жаңа тірек жоспарға көшеді немесе есептің шешілмейтіндігі орнатылады.
4. Бағыттаушы баған мен жолды табады. Бағыттаушы баған теріс санының абсолют шамасы бойынша үлкенін анықтайды, ал бағыттаушы жолды – Р0 вектор бағандарының компоненттері бағыттаушы бағанының оң компонеттеріне минималды арақатынасын анықтайды.
5. (4) – (7) формулалар бойынша жаңа тірек жоспарының оң компонеттерін, жаңа базис векторлары бойынша Pj векторының жіктелу коэффициенттерін және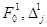 
сандарын анықтайды. Барлық сандар жаңа симплекс-кестеде жазылады.
6. Табылған тірек жоспарды оптималдылыққа зерттейді. Егер жоспар оптималды емес және жаңа тірек жоспарға көшу қажет болса, онда 4 этапқа қайта келу керек, ал оптималды жоспарды алған жағдайда есепті шешу процесі аяқталады.
Мысал: Р1 және Р2 өнімдерінің 2 түрін дайындау үшін S1, S2, S3, S4 ресурстарының төрт түрі пайдаланады.
| Ресурс түрлері | Ресурс қоры | Бір өнімді дайындауға кететін ресурстар бірлігінің саны | |
| Р1 | Р2 | ||
| S1 | |||
| S2 | |||
| S3 | - | ||
| S4 | - |
Р1 және Р2 өнімдерінің бірлігінен алынатын пайда сәйкесінше 2 және 3 теңге. Оны өндіруден пайда максималды болатындай өнімді өндірудің жоспарын құру керек.
| I | Базис | Сб | Р0 | Бағалаушы қатынас | ||||||
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | |||||
| Р3 | 18/3=6 | |||||||||
| Р4 | 16/1=16 | |||||||||
| Р5 | 5/1=5 | |||||||||
| Р6 | 21/0= 
| |||||||||
| m+1 | -2 | -3 | ||||||||
| Р3 | -3 | 3/1=3 | ||||||||
| Р4 | -1 | 11/2=5,5 | ||||||||
| Р2 |
| |||||||||
| Р6 | 21/3=7 | |||||||||
| m+1 | -2 | |||||||||
| Р1 | -3 |
| ||||||||
| Р4 | -2 | |||||||||
| Р2 | ||||||||||
| Р6 | -3 | 12/9 | ||||||||
| m+1 | -3 | |||||||||
| Р1 | -1/5 | 3/5 | ||||||||
| Р5 | -2/5 | 1/5 | ||||||||
| Р2 | 2/5 | -1/5 | ||||||||
| Р6 | 3/5 | -9/5 | ||||||||
| m+1 | 4/5 | 3/5 |
Оптималдылық критерийі орындалды, демек Ғmax=24. Оптмалды базистік шешім (6; 4; 0; 0; 1; 3).
Мысал №2: Әр түрлі А, В және С бұйымдарын дайындау үшін кәсіпорын шикізаттың үш түрін пайдаланады.
| Шикізат түрі | Бір бұйымға кететін шикізат шығынының нормасы (кг) | Шикізаттың жалпы саны (кг) | ||
| А | В | С | ||
| І ІІ ІІІ | ||||
| Бір бұйымның бағасы (тн) |
Сызықты программалаудың арнайы есептері. Тасымалдау (транспорт) есебі.
23. Транспорт есебінің қойылымы және математикалық моделі.
Тасымалдау есебінің жалпы қойылымы.
n-қойманың А1, А2,..., Аn әрқайсысында а1, а2,..., аn көлемінде жүк бар. Бұл жүкті m пайдаланушыға В1, В2,..., Вm қажетті мөлшерде b1, b2,..., bm жеткізуге тиіс және жұмсалатын қаржы берілген:
Бұл есептерде 2 критерий қарастырылады:
1. ең аз тасымалдауға жұмсалатын уақыт
2. ең аз тасымалдауға жұмсалатын қаржы
(1)
(2)
(3)
Осы есептің математикалық моделін қарастырған кезде, келесі жағдай болуы мүмкін.
1. 
. Бұл жағдайда математикалық модель жабық деп аталады.
2. 
. Бұл жағдайда математикалық модель ашық деп аталады. Есептеген кезде жалған пайдаланушыны қосамыз.
3. 
. Бұл жағдайда да математикалық модель ашық. Есептеген кезде жалған қоймаларды қосамыз.
Есептегенде толтырылған клеткалар саны r=m+n-1 рангке тең болу керек.
m – пайдаланушылар саны
n – қоймалар саны
Егер толтырылған клеткалар саны рангке тең болмаса, онда жоспар – ерекше деп аталады.
24. Транспорт есебінің ашық және жабық түрі, жабық түрге келтіру
Есептің математикалық моделін қарастырған кезде, келесі жағдай болуы мүмкін.
1. . Бұл жағдайда математикалық модель жабық деп аталады.
2. . Бұл жағдайда математикалық модель ашық деп аталады. Есептеген кезде жалған пайдаланушыны қосамыз.
3. . Бұл жағдайда да математикалық модель ашық. Есептеген кезде жалған қоймаларды қосамыз.
Есептегенде толтырылған клеткалар саны r=m+n-1 рангке тең болу керек.
m – пайдаланушылар саны
n – қоймалар саны
Егер толтырылған клеткалар саны рангке тең болмаса, онда жоспар – ерекше деп аталады.
Тасымалдау есептерінің бастапқы жоспарын анықтау үшін солтүстік-батыс бұрыш әдісі, ең кіші элемент әдісі және Фогель аппроксимациясы әдісі, ал оптималды жоспарды анықтау үшін потенциал әдісі қолданылады.
Мысалы: Қоймада 300, 250, 200 көлемінде үш түрлі А1, А2, А3 тауар бар. Бұл тауарды бес берілген В1, В2, В3, В4, В5 дүкендерге 210, 150, 120, 135, 135 көлемінде жеткізу керек. Жүкті тасымалдау үшін жұмсалатын қаржы:
Оптималды жоспарды анықтау керек.
Шешуі:
1. математикалық моделі
2. Бастапқы жоспар
Тасымалдау есебін кестеде есептеуге ыңғайлы.
а) Бұл тәсіл бойынша тасымалдау есебінің үлестіру кестесі оның жоғарғы сол жақ бұрышынан бастап толтырыла бастайды.
| Қойма | пайдаланушылар | Қоры | ||||
| В1 | B2 | В3 | B4 | B5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Қажеттілігі |
1) математикалық модель жабық;
2) r=m+n-1; r=5+3-1=7
Бұл жоспарды орындауға жұмсалатын қаржы мөлшері былайша анықталады:
Ғ=4*210+8*90+4*60+11*120+9*70+1*65+4*135=4355
б) Ең кіші элемент әдісі. Бұл әдісте кестенің толтырылуы ең кіші тарифтен басталады.
| Қойма | пайдаланушылар | Қоры | ||||
| В1 | B2 | В3 | B4 | B5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Қажеттілігі |
Ғ=4*145+8*20+7*135+4*130+11*120+3*65+1*135=3855
в) Фогель аппроксимациясы әдісімен есептеу
Енді тасымалдау есебінің ашық моделін жабық түрге келтіру жолдарын қарастырайық.
Мысал: Келесі тасымалдау есебі берілсін:
A=(200; 175; 225); B=(100; 110; 80; 190; 90)
Шешуі:
1. математикалық моделі
Теңсіздіктер санына байланысты қосымша белгісіздер енгізіледі:
Қосымша айнымалы шамаларды енгізудің экономикалық мәні мынандай: келесі мөлшерде жүк алатын жалған жүк алушы Вф енгізіледі.
Ал жүк бірлігін жалған жүк алушыға жеткізу құны нөлге тең деп есептелінеді:
Себебі жалған жүк алушының алатын х16 жүк мөлшері жүк берушілерде қалады. Онда есептің жабық моделінің кестесі келесі түрде болады:
| қойма | пайдаланушылар | Қоры | |||||
| В1 | B2 | В3 | B4 | B5 | Bф | ||
| А1 | |||||||
| А2 | |||||||
| А3 | |||||||
| Қажеттілігі |
Енді бұл есепті алдыңғы есеп сияқты шешуге болады.
25. Транспорт есебін шешу алгоритмі
1. Ашық тірек есебін жабық түрге келтіру.
2. Алғашқы тірек жоспарын құру.
- солтүстік батыс бұрыш, минимал әдіс арқылы шешу.
3. Оптималдыққа тексеру. Ол үшін
А) 
>0 жабық клеткалар үшін саны m+n-1 тең.
Б)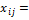 
0 ашық нөлдік клеткалар үшін
В)қандай да бір 
>0, - оптимал емес, онда тұйық контур тұрғызылады.
Max( 
) – төбесінен
d) min төбесі саны табылады.
e) сол санды «+» қосамыз:
«-» төбелерінен аламыз.
26. Транспорт есебінде алғашқы тірек жоспарын құру әдістері
Көлік есебін шешу үшін алған мәліметтерді 1-кестеге жинақтаймыз. Көлік есебінің шектеулер жүйлері сызықты тәуелді және m+n-1 айнымалы болуы керек және оны кесте мәліметтерінен оңай алуға болады. Қалған айнымалылар базистік емес және оладың мәндері нөлге тең. Кестеде ол нөлдерді көрсетпейміз, сондықтан ол тор көздер толтырылмайды.
Дата добавления: 2015-01-19; просмотров: 1019; Мы поможем в написании вашей работы!; Нарушение авторских прав |