Теңдеулер

Теңдеу деп белгісіз айнымалысы бар алгебралық өрнекті атаймыз. Теңдеулердің түрлері сан алуан- сызықты, квадраттық, тригонометрикалық, логарифмдік және тағы да сол сияқты.

Осы сайтта мынандай теңдеулер мен олардың шешімдері келтірілген:

1. Сызықты теңдеу.

Сызықты теңдеу деп a·x+b=c типті теңдеуді атайды, мұндағы a,b,c тұрақты сандар ал x ізделінетің белгісіз.

2. Сызықты теңдеулер жүйесі.

Мына жүйені сызықты теңдеулер жүйесі деп атайды:

мұндағы x пен y ізделінетін белгісіздер, ал белгілі тұрақты сандар.

3. Квадраттық теңдеу.

ax²+bx+c=0 теңдеуі квадраттық теңдеу деп аталады, мұндағы a,b,c тұрақты сандар ал x белгісіз айнымалы.

Жиын уғымы. Жиынның элементтері

Жиын ұғымы математикада негізгі (анықтауға болмайтын, бастапқы) ұғым болып саналады. Сондықтан оны тек мысылдармен ғана түсіндіруге болады. Мысалы, қайсыбір класс оқушыларының жиыны туралы, Әлемдегі планеталар жиыны туралы айтуға болады. «Жиын» сөзі математикада «жиынтық», «класс», «жинақ», «коллекция» деген сөздердің, яғни қайсыбір нәрселер жиынтығын сипаттайтын сөздердің орнына қолданылады, оның үстіне қарастырылып отырған жиынтықты бір ғана нәрсе болуы немесе бірде-бір нәрсе болмауы мүмкін.

Жиын құратын кез-келген нәрселер (адамдар, үйлер, кітаптар, елдер, геометриялық фигуралар, сандар т. б.) оның элементтері деп аталады. Мысалы, 3 саны - бір таңбалы натурал сандар жиынының элементі. Жиын мен оның элементтерінің арасындағы «элементті болады» деген байланысты «тиісті» сөзінің көмегімен де білдіруге болады. Мысалы, 3 саны бір таңбалы натурал сандар жиынына тиісті деп айтуға болады.

Соңғы сөйлемде символдың көмегімен қысқаша жазуға болады: 3ÏА. Бұл жазуда А әрпі арқылы бір таңбалы натурал сандар жиыны белгіленген (жиынды латын алфавитінің бас әріптерімен белгілейді), ал Îбелгісі «тиісті» сөзін алмастырады.

Жалпы аÎА жазуы «а нәрсесі А жиынының элементті», немесе «а нәрсесі А жиынына тиісті», немесе «А жиынында а элементі бар» деп оқылады. аÏА жазуын «а нәрсесі А жиынына тиісті емес», немесе «А жиынында а элементті жоқ», немесе «а нәрсесі А жиынының элементі емес» деп оқуға болады.

Жиын элементтерінің саны шектеулі де, шектеусіз болуы мүмкін. Мысалы, қайсыбір педучилище оқушыларының жиының элементтерінің саны шектеулі, ал түзудегі нүктелер жиыны шектеусіз.

Жиын ұғымы және онымен байланысты басқа да ұғымдар математиканы алғаш оқытудың негізі болады және онда кеңінен пайдаланылады. Кейбір оқулықтарда «жиын» термині кездеспейді, бірақ бұл ұғым айқындалмаған түрде пайдаланылады, ал бір қатар эксперимент кітаптарда жиын ұғымы символикасымен қоса айқын түрде пайдалалынылады. Сан, натурал сандарды қосу және көбейту амалдары және олардың қасиеттері, геометриялық фигура сияқты маңызды ұғымдардың қалыптасуы мектептегі математика курсында теориялық - жиындық негізде жүзеге асады.

Жиындардың жазылуы мен оның берілу тәсілдері

Егер әрбір нәрсе туралы оның жиынға тиісті немесе тиісті емес екендігін айта алатын болсақ, онда жиын берілген деп саналады.

Жиынды оның барлық элементтерін атау арқылы анықтап беруге болады. Егер де а, b, c, d - әр түрлі нәрселердің белгіленулері болса, онда осы нәрселердің жиынын А={ а, b, c, d } түрінде жазып, оны «А жиыны а, b, c, d элементтерінен тұрады» деп оқиды.

Әрбір нәрсе жиынға тек бір рет қана енеді. Мысалы, 32 545 882 санының әр түрлі цифрларынан тұратын жиын {3, 2, 5, 4, 8}, ал «есеп» деген сөздегі әр түрлі әріптер жиыны {e, c, п} түрінде жазылады.

Жиынның берілуінің тағы бір тәсілі оны құрайтын нәрселердің ортақ қасиетін атау болып табылады. Мұндай қасиетті cипаттамалық қасиет деп атайды. Мысалға, 7-ден кем натурал сандардың А жиынын қарастырайық. Бұл жерде А жиынының барлық элементтерінің ортақ қасиеті, атап айтқанда, олардың «натурал және 7-ден кіші сан болуы» аталып отыр. Қарастырылып отырған А жиынының элементтерін атап шығу қиындыққа түспейді: А={1, 2, 3 ,4, 5, 6}

Жиынның осылай берілу тәсілі математикада жиі қолданылады. Мысалға радиусы r, центрі О болатын шеңбердің «центрі О және радиусы r болатын шеңбер деп жазықтықтың О нүктесінен r қашықтықта жататын нүктелер жиынын атайды» деген анықтамасын еске түсірейік. О-дан r қашықтықта және бір жазықтықта жату - центрі О және радиусы r болатын шеңбердің барлық нүктелеріне тән қасиет және бұл қасиетке шеңберге тиісті емес бірде бір нүкте ие бола алмайды.

Элементтердің сипаттамалық қасиеті көрсетілген жиынды былай жазуға болады: фигуралық жақшалар ішіне алдымен элементтерінің белгіленуін жазады. Содан кейін вертикаль сызықша қояды да сызықшадан соң осы жиын элементтеріне және тек соларға ғана тән қасиетті жазады. Мысалы, 7-ден кіші натурал сандар жиыны А былайша жазылады:

А={x/x- натурал сан, x<7}

Сонымен, қандай да бір жиын берілген болуы үшін не оның элементтерін атап шығу, не оның элементтеріне тән қасиетті көрсету керек. Екінші тәсіл біріншіге қарағанда жалпылау екенін айта кетеміз. Мәселе мынада: жиынның элементтерін атап шығу осы жиын шектеулі болғанда ғана мүмкін, ал жиын элементтерінің ортақ қасиетін жиын шектеулі болғанда ғана мү мкін, ал жиын элементтерінің ортақ қасиетін жиын шектеулі болса да, шектеусіз болса да көрсетуге болады.

Бірақ кейбір кезде шектеусіз жиынды да бірінші тәсілді пайдаланып жазып көрсетуге болады. Мысалы, барлық натурал сандар жиынын N әрпі арқылы белгілеп мына түрде

N= {1, 2, 3, 4, …} жазуға болады.

Әрине жиынды тек көп нүктелер орнында не болатыны белгілі жағдайда ғана осы түрде жазуға болады.

Барлық натурал сандардан және нольден тұратын жиынды N₀ арқылы белгілеп, былай жазады:

N₀={1, 2, 3, 4, …}

Бұл жиынды оң бүтін сандар жиыны деп атайды.

Барлық бүтін сандар жиынын Z әрпі арқылы белгілеу келісілген: Z={…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5…}

Математиканы оқып-үйрену барысында шешуге тура келетін көптеген есептер элементтерінің ортақ қасиеті көрсетілген жиынды табумен байланысты болады. Бірнеше мысалдар келтірейік.

1-мысал.

х(х-1)=0 теңдеуінің барлық түбірлерінің жиынын табу керек.

Ізделінді А жиынының барлық элементтеріне тән ортақ қасиет -«х(х-1)=0 теңдеуінің түбірі болу», яғни А жиынын А={x| x(x-1)=0} түрінде жазуға болады. x(x-1)=0 - теңдеуін шешеміз. Екі х және х-1 сандарының көбейтіндісі, тек сол сандардың біреуі ноль болғанда ғана, нольге тең болатындықтан х₁=0, х₂=1 екендігін табамыз. Демек, А={0, 1}.

10 Сызықтық программалау есебінің стандарт, канондық және жалпы түрлері

немесе минималды мән қабылдаса, онда ол оптималды (тиімді) жоспар деп аталады. Егер (1.5) шектеулер жүйесі тек теңсіздіктерден тұратын болса, онда сызықтық бағдарламалау есебінің мұндай түрі стандартты (симметриялық) деп аталады; егер (1.5) шектеулер жүйесі тек теңдіктерден тұратын болса, онда

сызықтық бағдарламалау есебінің мұндай түрі канондық (негізгі) деп аталады.

(3) мақсатты функцияға максималды мән әперетін және (1) теңсіздік пен (2) шартты қанағаттандыратын өнімді шығару жоспарын табу керек.

Есептің жалпы түрі. айнымалысы бар сызықты теңдеулер жүйесі

(1)

және сызықты функция

. (2)

,(3)

берілген. (2) сызықты функциясына оптималды мән әперетін (яғни максималды немесе минималды) (1) теңсіздік пен (3) шартты қанағаттандыратын оптималды жоспарын табу керек.

(1) жүйе шектеулер жүйесі, ал функция - сызықты функция, мақсатты функция деп аталады.

Сызықты программалау есебінің оптимальды шешімі (немесе оптимальды жоспары) деп (2) сызықты функциясына оптималды мән әперетін (яғни максималды немесе минималды) (1) теңсіздік пен (3) шартты қанағаттандыратын шешімі аталады.

"Шешім" және "жоспар" – синонимдер, бірақ бірінші жиі қолданылады.

( ) теріс емес шарты орындалып, (1) шектеулер жүйесі тек теңсiздiктерден тұрса, онда ондай есеп стандартты деп аталып, ал тек теңдіктер жүйесінен тұратын шектеулер жүйесі канондық, яғни негізгі есеп деп аталады. Жоғарыда келтірілген есеп стандартты есеп.

Сызықты программалаудың кез-келген есебін жалпы, стандартты, канондық түрге келтіруге болады. Келесі мынадай теореманы қарастырайық.

Теорема 1.1. 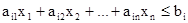(4)

теңсіздігінің кез келген әрбір шешіміне

(5)

мұндағы , (6) теңдеуінің анықталған әрбір шешімі сәйкес келеді және керісінше (5) теңдеудің және (6) теңсіздіктің шешіміне (4) теңсіздіктің әрбір шешімі сәйкес келеді.

Осы теореманы пайдаланып, стандартты есепті канондық түрге келтірейік. Ол үшін теңсіздіктер жүйесін теңдіктер жүйесіне ауыстырамыз. Яғни қосымша айнымалыларын енгіземіз. Онда теңсіздік белгісі £ болса, айнымалы қосылады, ³ болса, алынады. Сонда жүйе:

(1.4)

Осылайша, (1.1) стандартты есеп канондық түрде: (1.4) жүйесін және (1.2) шартын қанағаттандыратын, (1.3) функциясын максималды мән әперетін . шешімді табу керек.