
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Транспорттық есеп үшін потенциалдар тәсілінің алгоритмі
Есептің алгоритмі бірқатар мүмкін болатын базистік жоспарды таңдаудан басталады (мысалы, алдында солтүстік-батыс бұрыш тәсілі бойынша алынған алғашқы тасымалдау жоспары). Егер осы жоспар туындамаған болса, онда ол m+n-1 нольге тең емес базистік тордан тұрады, және оған қарап, әрбір базистік тор үшін (яғни xi,j > 0 торлар үшін)
vj-ui=ci,j, если xi,j>0, (5.5)
шарты орындалатындай ui и vj потенциалдарын анықтауға болады.
ui айнымалыларын өндіру орындарының потенциалдары деп, ал vj – тұтыну орнының потенциалдары деп талады.
Ол үшін vj-ui=ci,j тасымалдау жоспарының толтырылған (!) клтекалары үшін жүйе құру қажет, мұндағы ci,j – i пунктінен j пунктіне тасымалдау құны.
(6.5) жүйесі m+n-1 теңдеуден және m+n белгісізден тұратындықтан, потенциалдардың біреуін ойша беруге болады (мысалы, v1 немесе u1 нольге теңестіріп).
Одан кейін қалған vj және ui белгісіздері анық табылады.
Оптималдылық критериі.
Транспорттық есептің мүмкін болатын жоспары xi,j оптималды болуы үшін,
vj-ui=ci,j, егер xi,j>0,
vj-ui≤ci,j, егер xi,j=0 орындалатын ui, vj потенциалдары табылуы қажет және жеткілікті.
Жоспардың толтырылмаған (!) торлары үшін құндардың өзгеру коэффициентін анықтайық: dci,j = vj - ui - ci,j;
Есте сақтаңыз: егер барлық dci,j теріс болса, онда алынған жоспар оптималды болады. Егер dci,j кем дегенде біреуі оң болса, ары қарай [i,j] (dci,j>0 болғанда) торы жетекші (тіректі) болады.
Тасымалдаудың жаңа жоспарын анықтау үшін қайта санау циклін құрастыру қажет.
Қайт санау циклі соңдары толтырылған торларда жастқан, горизонталь және вертикаль сызықтардан тұратын тұйық үзілген қисық. Сынған сызық тіректі тордан басталады және аяқталады. Тіректі жоспардағы түйін оң боп саналады, келесісі теріс болып саналады және ары қарай кезектесе береді. Барлық теріс торларда мән алынады, ал оң торларда қосылады. Осымен, жаңа тасымалдау жоспарын алдық.
Цикл барлық dci,j теріс болмайынша, оптималды жоспар алынғанша жалғаса береді.
31. Транспорт есебінің тасымалдау жоспарының оптимал болу шарты
Метод потенциалов. Общий принцип определения оптимального плана транспортной задачи этим методом аналогичен принципу решения задачи линейного программирования симплексным методом, а именно: сначала находят опорный план транспортной задачи, а затем его последовательно улучшают до получения оптимального плана.
Оптималдылық критериі.
Транспорттық есептің мүмкін болатын жоспары xi,j оптималды болуы үшін,
vj-ui=ci,j, егер xi,j>0,
vj-ui≤ci,j, егер xi,j=0 орындалатын ui, vj потенциалдары табылуы қажет және жеткілікті.
Жоспардың толтырылмаған (!) торлары үшін құндардың өзгеру коэффициентін анықтайық: dci,j = vj - ui - ci,j;
Есте сақтаңыз: егер барлық dci,j теріс болса, онда алынған жоспар оптималды болады. Егер dci,j кем дегенде біреуі оң болса, ары қарай [i,j] (dci,j>0 болғанда) торы жетекші (тіректі) болады.
Тасымалдаудың жаңа жоспарын анықтау үшін қайта санау циклін құрастыру қажет.
Қайт санау циклі соңдары толтырылған торларда жастқан, горизонталь және вертикаль сызықтардан тұратын тұйық үзілген қисық. Сынған сызық тіректі тордан басталады және аяқталады. Тіректі жоспардағы түйін оң боп саналады, келесісі теріс болып саналады және ары қарай кезектесе береді. Барлық теріс торларда мән алынады, ал оң торларда қосылады. Осымен, жаңа тасымалдау жоспарын алдық.
Цикл барлық dci,j теріс болмайынша, оптималды жоспар алынғанша жалғаса береді.
Теорема 12.2 (критерий оптимальности). Для того чтобы допустимый план перевозок в транспортной задаче был оптимальным, необходимо и достаточно, чтобы существовали такие числа  и
и 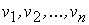 , что
, что  (12.4)
(12.4)
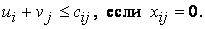 (12.5)
(12.5)
Числа  и
и 
 называют потенциалами пунктов отправления
называют потенциалами пунктов отправления  и назначения
и назначения 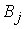 соответственно.
соответственно.
Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем. Пусть одним из рассмотренных выше методов найден опорный план. Для этого плана, в котором m + n – 1 базисных клеток, можно определить потенциалы  и
и  так, чтобы выполнялось условие (12.4). Поскольку система (12.4) содержит m + n – 1 уравнений и m + n неизвестных, то одну из них можно задать произвольно (например, приравнять к нулю). После этого из m+ n – 1 уравнений (12.4) определяются остальные потенциалы и для каждой из свободных клеток вычисляются величины
так, чтобы выполнялось условие (12.4). Поскольку система (12.4) содержит m + n – 1 уравнений и m + n неизвестных, то одну из них можно задать произвольно (например, приравнять к нулю). После этого из m+ n – 1 уравнений (12.4) определяются остальные потенциалы и для каждой из свободных клеток вычисляются величины  . Если оказалось, что
. Если оказалось, что 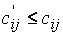 , то план оптимален. Если же хотя бы в одной свободной клетке
, то план оптимален. Если же хотя бы в одной свободной клетке  , то план не является оптимальным и может быть улучшен путем переноса по циклу, соответствующему данной свободной клетке.
, то план не является оптимальным и может быть улучшен путем переноса по циклу, соответствующему данной свободной клетке.
Циклом в таблице условий транспортной задачи, называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое – в столбце. Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами.
Процесс улучшения плана продолжается до тех пор, пока не будут выполнены условия (12.5).
Дата добавления: 2015-01-19; просмотров: 571; Мы поможем в написании вашей работы!; Нарушение авторских прав |