Сызықтық теңдеулер жүйесi

Мына түрдегi теңдеулердi ax=b, ax+by=c, ax+by+cz=d сәйкесiнше, бiр, екi, үш айнымалы (белгiсiздi) сызықтық теңдеулер дейдi, ал ax+byz=c сызықтық теңдеу болмайды. Өйткенi, ол айнымалыға қарағанда екiншi дәрежелi теңдеу.
n айнымалыны сызықтық теңдеудi қарастырайық. Оны былайша жазған жөн:
a ₁₁ x ₁ +a ₁₂ x ₂ +…+a _1n x=b (3.1)

Бұл теңдеудi дұрыс сандық теңдiкке айналдырайық:

x ₁ =l ₁ ,x ₂ =l ₂ ,…,x _n =l _n

сандарын (3.1) теңдеудiң шешiмi дейдi.
Егер n айнымалылы m сызықтық теңдеу берiлiп, айнымалының осы m теңдеудiң барлығын да қанағаттандыратын сан мәнiн табу керек болса, онда n айнымалылы m сызықтық теңдеулер жүйесi берiлген делiнедi. Оны әдетте, былайша жазады:

(3.2)

мұндағы x ₁ , x ₂ ,…,x _n - белгiсiздер (айнымалылар), a _ij (i=1,2,…,m; j=1,2,…,n) - белгiсiздiң коэффициенттерi, b ₁ , b ₂ ,…,b _m -босмүшелер делiнедi.
Белгiсiздердiң барлық теңдеулердi қатарынан қанағаттандыратын сан мәндерiнiң жиынын ол теңдеулер жүйесiнiң шешiмi дейдi. Ең болмағанда бiр шешуi бар жүйе үйлесiмдi, бiрде-бiр шешуi жоқ теңдеулер жүйесi үйлесiмсiз делiнедi.
Тек бiр шешiмi бар үйлесiмдi теңдеулер жүйесi анықталған, бiрден көп шешiмi бар теңдеулер жүйесi анықталмаған делiнедi.
(3.2) сызықтық теңдеулер жүйесiнiң коэффициенттерiнен жасалған матрицаны А арқылы, айнымалылардан және босмүшеден жасалған баған матрицаларды сәйкесiнше, х және В арқылы белгiлейiк:

,

Сонда (3.2) сызықтық теңдеулер жүйесi матрицалар арқылы былайша жазылады:

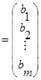
Сызықтық теңдеулер жүйесiнен айнымалыларының коэффициенттерiнен жасалған А матрицаны берiлген теңдеулер жүйесiнiң матрицасы дейдi, ал ол матрицаға босмүшенi бiр бағана етiп тiркеп жазғаннан шыққан матрицаны теңдеулер жүйесiнiң кеңейтiлген матрицасы дейдi де, арқылы белгiлейдi:

,

Сызықтық теңдеулер жүйесiнен үйлесiмдiлiгi және оның шешiмiнің саны туралы мынадай теоремалар бар:
1 ⁰ . (3.2) түрдегi сызықтық теңдеулер жүйесi үйлесiмдi болуы үшiн ол теңдеулер жүйесiнiң матрицасының рангi (rang A) мен кеңейтiлген матрицаның рангi (rang Ā) өзара тең болуы қажеттi және жеткiлiктi:

rang A= rang Ā (3.4)

Бұл тұжырым Кронекер-Капелли теоремасы делiнедi.
2 ⁰ . Егер (3.2) түрдегi сызықтық теңдеулер жүйесi үйлесiмдi болса, яғни rangA=rangĀ болса және ол теңдеулер жүйесiндiгi айнымалының санына тең болса:
rang A= rang Ā=n (3.5)

онда ол жүйенiң тек бiр шешуi болады, ал

rang A= rang Ā<n (3.6)

болса, теңдеулер жүйесiнiң шексiз көп шешуi болады.