Минимал элемент әдісі

Бұл әдістің ерекшелігі алғашқы таяныш жоспарын құрған кезде тасымалдау бағалары есепке алынады. xij мәні тасымалдың минималды бағасы бар тор көздерінен бастап анықталады.

Егер ондай тор көздер бірнешеу болса, онда олар бірінші тор көзден бастап кезекпен толтырылады. Жоспар алынған соң толтырылған тор көздер саны есептеледі. Егер олардың саны m+n-1 – ден кем болса, онда бос тор көздерге нөл жазылып, саны m+n-1 – ге жеткізіледі.

Жоғарыда көрсетілген әдістердің бірімен алынған алғашқы жоспар бірнеше әдістермен оптималдыққа тексеріледі. Солардың ішінде кең тарағаны үлестіру әдісі мен потенциалдар әдісі.

27. Транспорт есебінің ерекше және ерекше емес жоспарлары

Хij=0 нөлдік ашық клеткалар

Хij>0 жабық клеткалар

Егер жабық клеткалар n+m-1 болса, жоспар ерекше емес, ал егер Хij>0 саны <n+m-1 болса, онда жоспар ерекше жоспар деп аталады.

28. Транспорт есебін шешу әдісі

Потенциал әдісін 1949 жылы совет ғалымдары Л.В. Канторович пен М.К. Гавурин ойлап тапқан. Ол әдістің көмегімен алғашқы таяныш жоспардан саны шектеулі итерация жасай отырып көлік қатынас есебінің оптимал шешімін табуға болады. Потенциал әдісі көлік және осы тектес есептерді шығаратын үлестіру әдісінің жетілдірілген түрі болып табылады.

Потенциал әдісінің мағынасы әрбір жол және бағана үшін анықталатын

потенциал деп аталатын сандарда (potential - мүмкін). Потенциал көмегімен

кестедегі бос клеткаларды толтыруға болу, болмауын анықтауға болады. Потенциал әдісінің алгоритмі төмендегідей кезеңдерге бөлінеді:

1)Әрбір А1 жабдықтаушыға (жол) А1 потенциалдары деп аталатын B, Bj

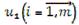сандары, ал тұтынушыларға потенциалдары деп аталатын, сандары сәйкес келеді.

Әрбір толтырылған клетка үшін, яғни базистік айнымалылар үшін

Алынған жүйе m+n белгісізі бар m+n-1 теңдеуден тұрады. Сондықтан бір потенциалға еркін мән беріледі. Мысалы u1=0 деп алып қалған потенциалдар табылады және олар кестенің жолдары мен бағандарына сәйкес оң және төменгі жағына жазылады.

2) Әрбір бос клетка үшін формуласы бойынша жанама тариф есептеліп, кестедегі бос клеткалардың төменгі сол жақ бұрышына жазылады.

3) Алынған жоспарды көлік қатынас есебінің оптималдығының критерийі бойынша оптималдыққа тексереміз. Егер барлық бос клеткалар үшін болса, онда жоспар оптималды болады. Егер бұл шарт орындалмаса, онда жоспар оптималды емес, 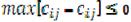шарты бойынша жаңа базистік жоспарға өтеміз.

4) Алынған бос клетка бойынша цикл (тізбек) құрамыз. Ол бос клеткадан

басталып қалған төбелері бос емес клеткаларда жатады.

5) Бос клеткаға « + » таңбасын, келесі клеткаға « - » кезектестіріп қойып

шығамыз. « - » таңбасы бар клеткалардың минималды шамасы анықталады.

« + » таңбасы бар клеткадағы жүк мөлшеріне сол шаманы қосып, « - » таңбасы бар клеткадағы шамалардан алып тастаймыз.

Алынған минималды шама базистен шығатын айнымалыға сәйкес келеді.

Жаңа базистік жоспар қайтадан оптималдыққа тексеріледі, яғни 1 кезеңнен қайталаймыз.

29. Потенциалдар әдісінде тұйық контур тұрғызу

Получив начальный опорный план перевозок, следует проверить его оптимальность и, если требуется, перейти к новому опорному плану с лучшим значением целевой функции. Для этого применяют метод потенциалов. Каждому ПО и каждому ПН сопоставляют соответственно величины и потенциалы этих пунктов ( ).

Для того чтобы некоторый опорный план транспортной задачи был оптимальным, необходимо и достаточно того, чтобы ему соответствовала система из чисел ( ), удовлетворяющих условиям:

, (10.4)

для базисных клеток ( и

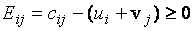, (10.5)

для пустых клеток ( .

Условия (10.4) и (10.5) называются условиями потенциальности.

Поскольку число неизвестных потенциалов всегда на единицу больше числа уравнений (числа базисных клеток) , то какое–либо одно из системы неизвестных , ( ) можно выбрать произвольно, например, равным нулю. Остальные потенциалы последовательно вычисляются из уравнений (10.4). Затем для всех свободных клеток из соотношений (10.5) определяются величины ( ) и, если все то полученный план перевозок является оптимальным. Если же имеются отрицательные , то план не оптимален и его следует оптимизировать.

10.3. Оптимизация плана перевозок

Среди пустых клеток с отрицательными значениями выбираем ту, у которой значение наименьшее. Эта пустая клетка рекомендуется к заполнению, в результате которого одна из базисных клеток становится пустой. Для этой пустой клетки строится цикл или контур, удовлетворяющий следующим условиям:

1) для каждой клетки можно построить единственный контур;

2) число вершин контура чётно;

3) все вершины контура, за исключением той, для которой он строится, находятся в клетках базисных неизвестных;

4) наиболее часто контур имеет вид прямоугольника, но возможны фигуры и другого типа (рис. 10.1)

Вершинам контура присваиваются чередующиеся знаки «+» и «−», начиная с той вершины, для которой этот контур строится. В вершинах контура, отмеченных знаком «−», выбирается наименьшее число и это число складывается с числами в вершинах, отмеченным знаком «+», и вычитается из чисел в вершинах, отмеченных знаком «−». При этом клетка с выбранной вершиной станет свободной, а клетка, для которой контур строился, – базисной.

Далее строится новая транспортная таблица и проверяется оптимальность плана. Если план перевозок оптимальный, получается оптимальное решение транспортной задачи; если нет, то план следует улучшать. Через определённое число последовательных шагов улучшения планов перевозок будет получен оптимальный план.

Рис. 10.1. Возможные циклы транспортной задачи линейного программирования

30. Потенциалдар әдісінің қолданысы

Метод потенциалов является модификацией симплекс-метода решения задачи линейного программирования применительно к транспортной задаче. Он позволяет, отправляясь от некоторого допустимого решения, получить оптимальное решение за конечное число итераций.

Метод потенциалов используется для решения транспортной задачи. Основой вычислительного процесса при улучшении опорного плана является определение критерия оптимальности d_ij:

d_ij = с_ij^* - с_ij,

где с_ij - затраты (истинные тарифы), связанные с доставкой одной единицы груза из i-того пункта отправления в j-ый пункт назначения; с_ij^* - расчётные затраты (косвенные тарифы), связанные с доставкой одной единицы груза из i-того пункта отправления в j-ый пункт назначения, определяемые для тех клеток опорного плана, ресурсы в которые не распределены (для незаполненных клеток).