Аралас стратегиялар

Теорема: Матрицалық ойын ойыншының төменгі бағасы ойыншының жоғарғы таза бағасынан аспайды, яғни а < β.

Егер матрица ойынның төменгі және жоғарғы бағалары сәйкес келсе, яғни а=βболса, онда бұл ойынның таза стратегиясында (седловая точка) ер нүктесі бар болады және V=а =β. і,j - таза стратегияның нөмірлері және а = β . А жөне В ойыншыларының осы теңціктерді қанағаттандыратын таза стратегиялардың сыңарларын (Аi,Вj) матрицалық ойыншының (седловой) ер нүктесі дейді, ал аіj элементін төлемдік матрицалық түйінді (седловой) элементі деп аталады. Онда : max min аij = minmax аij= а, бодады.

Төлемді матрицасы 2 түйінді элементтері бар а₁₂=2,а₁₄=2. Олай болса матрицалық ойындарда бірнеше түйіңді нүктелер бар(сәйкес түйінді элементке).

Сонымен В ойынншысы өзінің минмакстық стратегаясымен ауытқитын болса, онда оның ұтылысы көбейеді. Сол сияқты А ойыншы үшін минмакстық стратегия үтысын азайтады. Сонымен түйінді нүктедегі ойынның стратегиясы түрақтылық қасиетіне ие, олар тепе-тендік жағдайды туғызады. Бүдан шығатыны:

- Егер матрицалар ойынында түйіңді элемент болса, оңда ойыншы үшін ең қалаулысы таза стратегиялар болады. Соңцықтан Аі.,Вj таза стратегияларын , ойьшшылардың тиімді таза стратегиялары дейді.

Олай болса бұл өте қажетті тұжырым, ол былай болады:

Егер матрицалық ойынның түйінді элементі бар болса, оңда ол таза стратегияда шешіледі ; ал түйінді элементті күрасшртьш таза стратегия тиімді болады, ал ойынның шешімі деп (Ai,Bj,aij) үштігін айтады.

40. Аралас стратегияны анықтау әдісі (теңдеуі)

Егер матрицамен берілген ойында шешуші нүктесі жоқ болса, онда оның шешімін табу үшін аралас стратегия пайдаланылады. Ойын теориясында аралас стратегияны қолдану үшін төлем матрицаның көлемі 2х2 болуы керек.

Бірінші ойыншының аралас стратегиясын векторы ретінде, ал екінші ойыншының - векторы ретінде белгілейік, мұндағы ( ), ( ), , .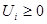

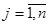Егер - бірінші ойыншының оптималды стратегиясы, ал 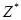- екінші ойыншының оптималды стратегиясы болса, онда саны ойын бағасы болып табылады. Мұндағы .

Теорема. Ойынның бағасы , ал және 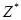- оптималды стратегиялар болу үшін төмендегі теңсіздіктердің орындалуы қажетті және жеткілікті:

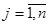( ) және ( ).

Теорема. Егер ойыншының біреуі оптималды аралас стратегия пайдаланса, онда оның ұтысы ойын бағасына тең болады.

Мысал 1: Матрицамен берілген ойынның шешімін табу және геометриялық интерпретациясын беру керек.

Шешуі:

	В1	В2
А1
А2

А ойыншыға стратегия векторымен берілсін.

мен қатысты екі жазылған теңдеуден тыс мен жиіліктерін байланыстыратын теңдеуді қосамыз:

;

Енді В ойыншыға оптималды стратегияны табу керек. Берілген ойыншыға стратегия векторымен берілсін. Сонда

Демек, ойынның шешімі аралас стратегиялар 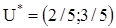және 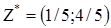, ал ойынның бағасы болып табылады.