Дисконтирование по сложной ставке

Из формулы (3.1) получим:

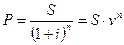, (3.10)

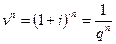. (3.11)

Величину v называют дисконтным (учетным, дисконтирующим) множителем. При начислении процентов m раз в году получим:

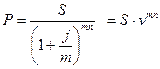; (3.12)

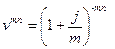. (3.13)

Величина P – современная (текущая) стоимость величины S. Разность S – P, когда P определено дисконтированием, называют дисконтом:

.

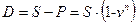Пример 3.10. Сумма в 5 млн. руб. выплачивается через 5 лет. Необходимо определить ее современную величину при условии, что применяется ставка сложных процентов, равная 12 % годовых.

Дисконтный множитель равен

.

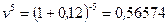Т. о., первоначальная сумма сократилась почти на 44 %. Современная величина равна:

тыс. руб. [5, с. 53–54].

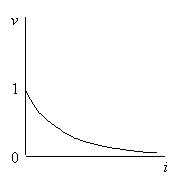Рис. 3.4. Зависимость дисконтного множителя от процентной ставки

С увеличением срока платежа величина современной стоимости убывает. Например, при ставке 12 % получим:   n 10 лет 50 лет 100 лет v 0,32197 0,00346 0,000012

Операции со сложной учетной ставкой