
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Наращение по сложной учетной ставке
Иногда наращенную сумму получают и с помощью сложной учетной ставки. Из (3.14) и (3.15) следует:
 , (3.16)
, (3.16)
 . (3.17)
. (3.17)
Множитель наращения при использовании сложной учетной ставки d равен [5, с. 57]
 .
.
3.6. Сравнение интенсивности процессов наращения
и дисконтирования по разным видам процентных ставок
Для решения поставленной задачи достаточно сопоставить соответствующие множители наращения (дисконтирования). Считаем размеры ставок одинаковыми.
Имеют место следующие соотношения для множителей наращения:
 при
при  ,
,
 при n = 1,
при n = 1,
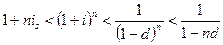 при n > 1.
при n > 1.
Видно, что соотношение множителей наращения зависит от сроков наращения процентов.
Пример. Множители наращения для разных видов ставок (20 %).
| Срок (в годах) | is | i | ds | d |
| 0,5 | 1,10 | 1,0954 | 1,1111 | 1,1180 |
| 1,0 | 1,20 | 1,2000 | 1,2500 | 1,2500 |
| 2,0 | 1,40 | 1,4400 | 1,6667 | 1,5625 |
| 10,0 | 11,00 | 6,1917 | ∞ | 9,3132 |
Соотношения для дисконтных множителей следующие:
 при
при  ,
,
 при n = 1,
при n = 1,
 при n > 1 [5, с. 57–58].
при n > 1 [5, с. 57–58].
Дата добавления: 2015-01-29; просмотров: 249; Мы поможем в написании вашей работы!; Нарушение авторских прав |