Финансовая эквивалентность обязательств

На практике нередко возникают случаи, когда нужно заменить одно денежное обязательство другим, например, с более отдаленным сроком платежа, или объединить несколько платежей в один и т. д. Такие задачи решают на основе принципа финансовой эквивалентности обязательств. Эквивалентными считаются такие платежи, которые, будучи «приведенными» к одному моменту времени, оказываются равными. Приведение осуществляется путем дисконтирования (приведение к более ранней дате) или, наоборот, наращения платежа (если дата относится к будущему). Если при изменении условий контракта указанный принцип не соблюдается, то одна из сторон контракта терпит ущерб, размер которого можно заранее определить.

Принцип финансовой эквивалентности лежит в основе значительного числа методов количественного финансового анализа. В наиболее простом проявлении этот принцип следует из формул наращения и дисконтирования, связывающих величины P и S. Сумма P эквивалентна сумме S при принятой процентной ставке и методе начисления процентов.

Две суммы S₁ и S₂, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы. Замена S₁ и S₂ в этих условиях формально не изменяет отношения сторон договора [5, с. 73].

Пример 4.7. На принципе эквивалентности основывается сравнение разновременных платежей. Имеется два обязательства. Условия первого: выплатить 400 тыс. руб. через 4 месяца; условия второго: выплатить 450 тыс. руб. через 8 месяцев. Можно ли считать их равноценными?

Т. к. платежи краткосрочные, то при дисконтировании на начало срока применим простую ставку, равную, допустим, 20 %. Получим:

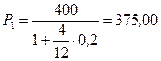тыс. руб.

тыс. руб.

Т. о., сравниваемые обязательства не являются эквивалентными при заданной ставке и в силу этого не могут адекватно заменять друг друга.

Сравнение платежей предполагает использование некоторой процентной ставки и, следовательно, его результат зависит от ее величины. Однако, что практически весьма важно, эта зависимость не является столь жесткой, как это может показаться на первый взгляд. Допустим, сравниваются 2 платежа S₁ и S₂ со сроками n₁ и n₂, причем, S₁ < S₂ и n₁ < n₂. Соотношение их современных стоимостей P₁ и P₂ зависит от размера процентной ставки i (см. рис. 4.2).

Рис. 4.2

С ростом i размеры современных стоимостей Р₁ и Р₂ уменьшаются, причем при i = i₀ выполняется Р₁ = Р₂. Для любой ставки i < i₀ выполняется Р₁ < Р₂. Т. о., результат сравнения зависит от размера ставки, равного i₀. Эта ставка называется критической (барьерной). Ее можно найти из равенства:

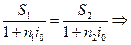
. (4.27)

Пример 4.8. Для данных примера 4.7 получим

, или 42,8 %.

Т. о., соотношение P₂ > P₁ справедливо при любом уровне процентной ставки, который меньше 42,8 %.

Если дисконтирование производится по сложной ставке, то критическую ставку найдем из равенства

.

Получим [5, с. 74–76]

. (4.28)