Определение срока консолидированного платежа

Если задана величина консолидированного платежа S₀, то возникает задача определения его срока n₀. В этом случае уравнение эквивалентности удобно представить в виде равенства современных стоимостей соответствующих платежей.

При применении простой ставки это равенство имеет вид:

,

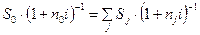откуда

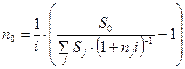. (4.31)

Очевидно, что решение можно получить при условии, что , иначе говоря, размер заменяющего платежа не может быть менее суммы современных стоимостей заменяемых платежей. Заметим также, что искомый срок пропорционален величине консолидированного платежа.

Пример 4.11. Суммы в размере 10, 20 и 15 млн. руб. должны быть выплачены через 50, 80 и 150 дней соответственно. Стороны согласились заменить их одним платежом в размере 50 млн. рублей. Найти срок платежа.

Современная стоимость заменяемых платежей (обозначим ее через P) при условии, что ставка i = 10 % и K = 365 дней, составит

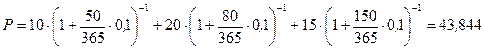млн. руб.

По формуле (4.31) находим

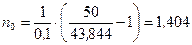года = 512 дней.

Если размер заменяющего платежа задан в сумме 45 млн. руб., то срок сократится и составит 0,264 года = 96 дней.

Для определения срока консолидированного платежа на основе сложных процентных ставок уравнение эквивалентности запишем следующим образом:

.

Для упрощения дальнейшей записи примем:

.

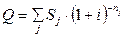После этого находим

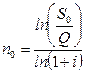. (4.32)

Решение существует, если S₀ > Q. Для частного случая, когда , при определении срока консолидированного платежа иногда вместо (4.32) применяют средний взвешенный срок:

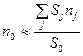. (4.33)

Привлекательность этой формулы в том, что она не требует задания уровня процентной ставки. Но надо помнить, что она дает приближенный результат, который больше точного. Чем выше ставка i, тем больше погрешность решения по формуле (4.33).

Пример 4.12. На основе данных примера 4.10 определить срок консолидированного платежа в сумме 3 млн. руб.

Точное значение срока находим по формуле (4.32). Для этого сначала рассчитаем Q:

млн. руб.

После этого находим

года.

Приближенное решение по формуле (4.33) дает:

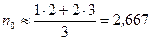года [5, с. 77–79].