F(x1, x2,...xm) const 6 страница

многоэкстремальных унимодальных линейных

в списке нет правильного ответа

За точку минимума при выполнении условия |bn - an|< можно принять

один из концов конечного отрезка [an;bn] в списке нет правильного ответа только середину отрезка

любую точку конечного отрезка [an;bn]

Значение для метода золотого сечения при решении задачи одномерной оптимизации на отрезке неопределенности [0;2] равно

1

0.382

нет правильного ответа

0.618

Всякий глобальный минимум выпуклой функции является одновременно и

нет правильного ответа локальным

точкой перегиба

максимумом

Первая производная от целевой функции на отрезке неопределённости должна

не убывать

монотонно возрастать или убывать быть постоянной монотонно убывать

Точность метода прямого перебора при решении задачи одномерной оптимизации повышается, если

увеличить шаг перебора нет правильного ответа

увеличить отрезок неопределенности

Функция, для которой решается задача оптимизации, называется

целевой дискретной векторной оптимальной

Вид функции на скорость сходимости метода дихотомии при решении задачи одномерной оптимизации

влияет, чем круче функция, тем быстрее сходимость для пологих функций сходимость ниже

не влияет

в списке нет правильного ответа

Глобальный минимум - это

наименьшее значение функции в некоторой окрестности в списке нет правильного ответа

один из минимумов функции в области допустимых значений

наименьший из минимумов в области допустимых значений

Коэффициенты золотого сечения равны при решении задачи одномерной оптимизации

0.5 и 0.5

1 и 2

0.382 и 0.618

0.318 и 0.682

Метод одномерной оптимизации, который требует проведения большего количества итераций для достижения заданной точности, это метод

золотого сечения

нет правильного ответа дихотомии

прямого перебора

Метод дихотомии при решении задачи одномерной оптимизации гарантирует отыскание минимума

в списке нет правильного ответа

если правильно выбран отрезок неопределенности

в некоторых случаях сходимость метода не гарантируется всегда

Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [6;8], методом золотого сечения с точностью 10-3 равно

n = 18

n = 19 n = 14

n = 15

Метод одномерной оптимизации, который обладает наименьшей трудоемкостью - это метод

золотого сечения прямого перебора

нет правильного ответа дихотомии

Методы одномерного поиска при решении задачи одномерной оптимизации применяются для функций

унимодальных линейных

в списке нет правильного ответа многоэкстремальных

Метод одномерной оптимизации, где проводится большее количество вычислений функции для достижения необходимой точности - это метод

дихотомии

Эйлера золотого сечения

нет правильного ответа

Суть методов одномерной оптимизации заключается

в списке нет правильного ответа

в увеличении отрезка неопределенности

в получении экстремального значения функции

в том, что на каждой итерации отрезок неопределенности уменьшается и стягивается к точке минимума

Глобальный минимум является

в списке нет правильного ответа первым по порядку из локальных наименьшим из локальных

наибольшим из локальных

Длина отрезка неопределенности [a;b] на следующей итерации в методе дихотомии при решении задачи одномерной оптимизации составляет

0.618(b–a)

0.5(b–a)

0.382(b–a)

0.2(b–a) Процесс выбора наилучшего варианта из всех возможных - это

интерполяция

в списке нет правильного ответа оптимизация

аппроксимация

минимизация

За решение задачи одномерной оптимизации при выполнении условия как правило принимают

в списке нет правильного ответа середину отрезка [ai;bi]

один из концов отрезка [ai;bi]

любую точку отрезка [ai;bi]

Методом оптимизации можно найти глобальный минимум, если

применять метод прямого перебора на отрезке только один минимум

глобальный минимум совпадает с локальным в списке нет правильного ответа

В каком методе при решении задачи одномерной оптимизации для достижения одного и того же значения погрешности требуется меньше итераций:

количество итераций будет одинаковым золотого сечения

дихотомии

В методе золотого сечения при решении задачи одномерной оптимизации на каждой итерации функция вычисляется один раз, потому что

в списке нет правильного ответа

одно из значений функции не вычисляется, а переопределяется, поскольку каждая из внутренних точек (х1 и х2) делят отрезок в соотношении золотого сечения

в методе золотого сечения от итерации к итерации один из концов интервала не изменяется

исходя из расчетных формул

В методе золотого сечения при решении задачи одномерной оптимизации на каждой итерации длина отрезка неопределенности [a;b] уменьшается

на 0.618(b–a) в 1.618 раз на 0.5(b–a)

в 0.618 раз

Функция на отрезке [1;3]

имеет единственный минимум не имеет точек экстремума имеет единственный максимум имеет минимум и максимум

Значение для метода золотого сечения при решении задачи одномерной оптимизации на отрезке неопределенности [0;2] равно

0.382

0.618

нет правильного ответа

Длина отрезка неопределенности в методе золотого сечения при решении задачи одномерной оптимизации сокращается на каждой итерации

в 2 раза

в 0.382 раза в 0.618 раз

нет правильного ответа

Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [0;1], методом золотого сечения с точностью 10-3 равно

n = 14 n = 19 n = 10 n = 15

Функция имеет локальный минимум в точке

[-1,-0.5]

[-0.25,0]

нет правильного ответа

[0,1]

Точка [0,-0.1] является точкой локального минимума функции

нет правильного ответа

Поиск минимума в методе дихотомии начинается с выбора на отрезке неопределённости

трёх произвольных точек нахождения середины

двух симметричных относительно середины точек

Вид функции на скорость сходимости метода прямого перебора при решении задачи одномерной оптимизации

в списке нет правильного ответа

чем круче функция, тем медленнее сходимость влияет

у пологих функций сходимость выше

Наиболее рациональным способом выбора параметра в методе дихотомии при решении задачи одномерной оптимизации является

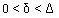
нет правильного ответа

Функция имеет минимум на отрезке

[0.2;1] [5;6]

нет правильных ответов

[-10;-9]

За точку минимума при выполнении условия |bn - an|< можно принять

в списке нет правильного ответа любую точку конечного отрезка [an;bn] один из концов конечного отрезка [an;bn] только середину отрезка

Условие существования минимума для функции от двух переменных - это

положительная определенность матрицы первых производных положительная определенность матрицы вторых производных матрица вторых производных равна нулю

отрицательная определенность матрицы вторых производных

Наименьшее значение функции в некоторой окрестности - это

локальный минимум нет правильного ответа глобальный минимум оптимальное значение

Количество итераций, необходимых для того, чтобы обеспечить заданную точность по методу дихотомии при решении задачи одномерной оптимизации, если , равно

1

нет правильного ответа

2

Первая производная от целевой функции на отрезке неопределённости должна

не убывать

монотонно возрастать или убывать быть постоянной монотонно убывать

Критерием унимодальности функции на заданном отрезке является тот факт, что

все перечисленные

функция дифференцируема, и вторая производная не отрицательна на этом отрезке функция дифференцируема, и первая производная не убывает на этом отрезке функция дифференцируема, и первая производная не отрицательна на этом отрезке

функция дважды дифференцируема, и первая производная не убывает на этом

отрезке

функция дважды дифференцируема, и вторая производная не убывает на этом отрезке

Для функции f(x,y) = точкой минимума является

(-0.3;0) (-0.2;0) (0.4;1) (0;0)

Достаточным условием существования минимума функции нескольких переменных является

матрица вторых производных должна быть положительно определена равенство нулю матрицы вторых производных

равенство нулю градиента функции

отличие от нуля матрицы вторых производных

отличие от нуля градиента функции

Метод одномерной оптимизации, который обладает более высокой скоростью сходимости - это метод

золотого сечения

нет правильного ответа прямого перебора дихотомии

монотонна

является

уравнением, содержащим производную интегральным уравнением

обыкновенным дифференциальным уравнением 1-го порядка квадратным уравнением

Геометрической интерпретацией общего решения ОДУ png]imgN1135.png] является

две пересекающиеся прямые

в списке нет правильного ответа семейство непересекающихся интегральных кривых две пересекающиеся кривые

Численное решение ОДУ представляет собой таблицу значений искомой функции для заданной последовательности аргументов, где называется

порядком уравнения нет правильных вариантов степенью функции

шагом интегрирования

Правильной записью приближенного числа является

Уменьшение шага интегрирования при использовании методов Рунге-Кутты (ОДУ)

уменьшает погрешность не влияет на погрешность увеличивает погрешность