F(x1, x2,...xm) const 3 страница

1. Значения точек

х1 и

х2 , вычисленные по методу золотого сечения на первой

итерации, при поиске минимума функции, на отрезке неопределенности [5,5.5]

равны…

1) x1 = 5.309, x2 = 5.191; *

2) x1 = 5.260, x2 = 5.240;

3) x1 = 5.447, x2 = 5.353;

4) x1 = 5.147, x2 = 5.053.

2. Значения точек

х1 и

х2 , вычисленные по методу дихотомии на первой итерации, с

при поиске минимума функции, на отрезке неопределенности [-1,0] (

равны…

0,01)

1) x1 = -0.49, x2 = -0.51; *

2) x1 = -0.48, x2 = -0.52;

3) x1 = -0.38, x2 = -0.62;

4) x1 = 0.49, x2 = 0.51;.

3. Значения точек

х1 и

х2 , вычисленные по методу золотого сечения на первой

итерации, при поиске минимума функции, на отрезке неопределенности [10,12]

равны…

1) x1 = 11.236, x2 = 10.764; *

2) x1 = 11.364, x2 = 10.636;

3) x1 = 11.011, x2 = 10.099;

4) x1 = 11.005, x2 = 10.995.

4. Значения точек

х1 и

х2 , вычисленные по методу дихотомии на первой итерации, при

поиске минимума функции, на отрезке неопределенности [-2,-1.5] (

1) x1 = -1.74, x2 = -1.76; *

2) x1 = -1.69, x2 = -1.81;

3) x1 = -1.73, x2 = -1.77;

4) x1 = -1.59, x2 = -1.61.

0,01) равны…

5. Значения точек

х1 и

х2 , вычисленные по методу золотого сечения на первой

итерации, при поиске минимума функции, на отрезке неопределенности [1.5,2]

равны…

1) x1 = 1.809, x2 = 1.691; *

2) x1 = 1.841, x2 = 1.659;

3) x1 = 1.761, x2 = 1.749;

4) x1 = 1.755, x2 = 1.745.

6. Значения точек х1 и х2 , вычисленные по методу дихотомии на первой итерации, при

поиске минимума функции, на отрезке неопределенности [-1,1] (

1) x1 = 0.01, x2 = -0.01; *

2) x1 = 0.24, x2 = -0.24;

3) x1 = 0.36, x2 = -0.36;

4) x1 = 0.02, x2 = -0.02.

0,01) равны…

7. Значения точек

х1 и

х2 , вычисленные по методу золотого сечения на первой

итерации, при поиске минимума функции, на отрезке неопределенности [0.5,0.8]

равны…

1) x1 = 0.685, x2 = 0.615; *

2) x1 = 0.705, x2 = 0.595;

3) x1 = 0.655, x2 = 0.645;

4) x1 = 0.747, x2 = 0.653.

8. Значения точек х1 и

х2 , вычисленные по методу дихотомии на первой итерации, при

поиске минимума функции, на отрезке неопределенности [1,1.5] (

1) x1 = 1.26, x2 = 1.24; *

2) x1 = 1.31, x2 = 1.19;

3) x1 = 1.34, x2 = 1.16;

4) x1 = 1.27, x2 = 1.23.

0,01) равны…

9. Значения точек

х1 и

х2 , вычисленные по методу золотого сечения на первой

итерации, при поиске минимума функции, на отрезке неопределенности [0,0.8]

равны…

1) x1 = 0.494, x2 = 0.306; *

2) x1 = 0.546, x2 = 0.254;

3) x1 = 0.414, x2 = 0.391;

4) x1 = 0.405, x2 = 0.395.

10. Значения точек

х1 и

х2 , вычисленные по методу дихотомии на первой итерации, с

целью нахождения точки минимума функции, на отрезке неопределенности [1.6,2]

( 0,01) равны…

1) x1 = 1.81, x2 = 1.79; *

2) x1 = 1.85, x2 = 1.75;

3) x1 = 1.87, x2 = 1.73;

4) x1 = 1.82, x2 = 1.78.

11. Длина отрезка неопределенности после 10-ти итераций по методу дихотомии

( 0,01), если минимум отделен на отрезке [4,5], равна…

1) 0.021; *

2) 0.011;

3) 0.192;

4) 0.356.

12. Длина отрезка неопределенности после 5-ти итераций по методу дихотомии

( 0,001), если минимум отделен на отрезке [3,5], равна…

1) 0.064; *

2) 0.28;

3) 0.812;

4) 0.127.

13. Длина отрезка неопределенности после 10-ти итераций по методу золотого сечения, если минимум отделен на отрезке [3,5], равна…

1) 0.016; *

2) 0.222;

3) 0.124

4) 0.026.

14. Длина отрезка неопределенности после 6-ти итераций по методу золотого сечения, если минимум отделен на отрезке [2,4], равна…

1) 0.111; *

2) 0.051;

3) 0.201;

4) 0.099.

15. Длина отрезка неопределенности после 5-ти итераций по методу дихотомии

( 0,01), если минимум отделен на отрезке [2,5], равна…

1) 0.113; *

2) 0.103;

3) 0.270;

4) 0.098.

16. Длина отрезка неопределенности после 3-х итераций по методу дихотомии (

если минимум отделен на отрезке [0.1,0.6], равна…

1) 0.08; *

2) 0.23;

3) 0.33;

4) 0.56.

0,01),

17. Длина отрезка неопределенности после 4-х итераций по методу золотого сечения, если минимум отделен на отрезке [0.5,0.6], равна…

1) 0.015; *

2) 0.022;

3) 0.025;

4) 0.011.

18. Длина отрезка неопределенности после 3-х итераций по методу золотого сечения, если минимум отделен на отрезке [5,7], равна…

1) 0.472; *

2) 0.634;

3) 0.111;

4) 0.268.

19. Длина отрезка неопределенности после 5-ти итераций по методу дихотомии

( 0,01), если минимум отделен на отрезке [5,7], равна…

1) 0.082; *

2) 0.180;

3) 0.016;

4) 0.072.

20. Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [2,4], методом золотого сечения с точностью 10-4 равно…

1) n = 20; *

2) n = 16;

3) n = 25;

4) n = 19.

21. Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [0,1], методом золотого сечения с точностью 10-3 равно…

1) n = 15; *

2) n = 19;

3) n = 10;

4) n = 14.

22. Теоретическое количество итераций, необходимое для локализации точки минимума,

отделенного на отрезке [0,1], методом дихотомии (

равно…

0,0001) с точностью 10-3

1. n = 11; *

2. n = 10;

3. n = 14;

4. n = 12.

23. Теоретическое количество итераций, необходимое для локализации точки минимума,

отделенного на отрезке [1,3], методом дихотомии (

1) n = 8; *

2) n = 7;

3) n = 9;

4) n = 10.

0,001) с точностью 10-2 равно…

24. Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [6,8], методом золотого сечения с точностью 10-3 равно…

1) n = 15; *

2) n = 14;

3) n = 18;

4) n = 19.

25. Теоретическое количество итераций, необходимое для локализации точки минимума,

отделенного на отрезке [1,2], методом дихотомии (

1) n = 6; *

2) n = 7;

3) n = 9;

4) n = 8.

0,001) с точностью 10-2 равно…

Методы решения задачи безусловной минимизации в действительности являются методами поиска

точки локального минимума градиента функции антиградиента функции длины шага

Корень уравнения f(x)=0 считается отделенным на отрезке [a;b], в котором содержится

4 корня

3 корня

1 корень

2 корня

Задача нахождения корня уравнения с заданной точностью считается решенной, если

Нахождение возможно более узкого отрезка, содержащего только один корень уравнения, называется

уточнением корней разделением корней

решением нелинейного уравнения отделением корней

Начальное приближение к корню - это

значение х, являющееся одним из концов отрезка, содержащего корень значение х, при котором уравнение обращается в тождество значение х, принадлежащее отрезку, содержащему корень

значениe х, обеспечивающее сходимость метода уточнения корня

В точке корня функция равна

нулю бесконечности значению корня значению функции

Первая производная от целевой функции на отрезке неопределённости должна

не убывать монотонно убывать

монотонно возрастать или убывать

быть постоянной

Процесс выбора наилучшего варианта из всех возможных - это

минимизация

в списке нет правильного ответа интерполяция

оптимизация

аппроксимация

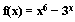Отрезок неопределенности для функции равен

[-5;-4]

нет правильного ответа

[2;3]

[-9;-8]

Длина интервала неопределенности после 2 итерации по методу золотого сечения при решении задачи одномерной оптимизации, если , равна

2

нет правильного ответа

0.381924

0.617934

Значение для метода золотого сечения при решении задачи одномерной оптимизации наи отрезке неопределенности [1;2] равно

1.382

2.382

0.382

0.618

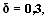Минимальное значение функции на отрезке [0;1] c точностью и параметра равно

0.5

0.7

0.2

0.6

Из перечисленных методов к методам многомерной оптимизации относятся

метод Гаусса метод Рунге-Кутта

метод Симпсона

в списке нет правильного ответа

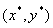Если - единственное решение, то в этой точке

все угловые миноры были положительны все миноры были положительны

все угловые миноры были отрицательные все угловые миноры были равны 0

Методы спуска при решении задачи многомерной оптимизации с использованием градиента функции различаются выбором

начальной точки рекуррентной формулы параметра направления градиента

Множество точек, для которых целевая функция принимает постоянное значение

, называется

траекторией спуска

в списке нет правильного ответа градиентом

поверхностью уровня

Согласно критерию Сильвестра, для того, чтобы матрица была положительно определена, необходимо, чтобы

все угловые миноры были положительны все миноры были положительны

все угловые миноры были отрицательные все угловые миноры были равны 0

Антиградиент функции показывает

скорость убывания функции скорость возрастания функции

направление наискорейшего убывания функции

направление наискорейшего возрастания функции

Градиент функции f(x,y) – это

скалярная функция векторная функции число

вектор

Методы спуска применяются для минимизации функций только от

одной переменной

не применяются для минимизации нескольких переменных

Траектория спуска - это

множество точек, для которых целевая функция принимает постоянное значение в списке нет правильного ответа

последовательность точек , получаемых методом спуска

последовательность значений целевой функции, получаемых методом спуска

Суть метода наискорейшего спуска при решении задачи многомерной оптимизации состоит в том, что из выбранной точки спуск осуществляется в направлении антиградиента, до тех пор, пока не будет достигнуто

среднее значение целевой функции вдоль луча максимальное значение целевой функции вдоль луча нулевое значение целевой функции вдоль луча минимальное значение целевой функции вдоль луча

На каждой итерации в методе наискорейшего спуска при решении задачи многомерной оптимизации шаг выбирается исходя из условия

в списке нет правильного ответа максимума целевой функции минимума целевой функции равенства нулю целевой функции

очка x для которой выполняется равенство =0 называется

глобальной точкой функции локальной точкой функции экстремальной точкой функции

стационарной точкой функции

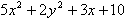Для функции f(x,y) = матрица Гессе имеет следующий вид

Поиск очередной точки траектории спуска в методе наискорейшего спуска при решении задачи многомерной оптимизации осуществляется

в направлении градиента

в направлении антиградиента

в направлении оптимального значения целевой функции в списке нет правильного ответа

Градиентные методы – это методы, в которых движение к точке минимума совпадает с направлением

вектора градиента функции одной из координат осей вектора антиградиента функции в списке нет правильного ответа

Если для всей области допустимых значений выполняется неравенство то точка x*

являеться точкой

локального максимума глобального минимума нет правильного ответа экстремума

Метод спуска при решении задачи многомерной оптимизации – это метод, для которого каждая итерация (шаг) приводит

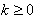к уменьшению целевой функции , для всех

к тому, что целевая функция не меняется , для всех к увеличению целевой функции , для всех

в списке нет правильного ответа

Метод одномерной оптимизации в численном методе наискорейшего спуска (НСЧ) при решении задачи многомерной оптимизации используется

для нахождения точки минимума

для вычисления минимума модуля градиента для выбора величины шага спуска

для обеспечения точности поиска минимума

Чтобы с использованием метода наискорейшего спуска найти максимум функции f(x1, x2) нужно

выбрать в качестве направления поиска направление вектора градиента найти минимум функции и взять его с противоположным знаком

в списке нет правильного ответа

заменить в расчетах знак у целевой функции на противоположный

Отличие численного метода наискорейшего спуска при решении задачи многомерной оптимизации состоит в том, что поиск значения на каждой итерации происходит

одним из численных методов одномерной оптимизации методом конфигураций

аналитическим методом методом штрафных функций

В градиентных методах при решении задачи многомерной оптимизации для определения координат следующей точки необходимо знать

только шаг

направление, на котором расположена точка и шаг начальную точку и шаг

только направление, на котором расположена точка

Из перечисленных понятий к методам многомерной оптимизации относится

правило Рунге метод Сильвестра метод Гаусса

метод покоординатного спуска

Условие окончания итерационного процесса по отысканию точки минимума в методах спуска - это

модули частных производных по всем переменным больше заданной точности в списке нет правильного ответа

частные производные по всем переменным равны нулю

модули частных производных по всем переменным меньше заданной точности

Выпуклыми матрицами Гесса являются следующие

Метод, позволяющий избежать «овражного» эффекта при решении задачи многомерной оптимизации - это

метод ГДШ

метод наискорейшего спуска метод НСА

метод покоординатного спуска

Вектор антиградиента направлен

в сторону наискорейшего возрастания целевой функции в сторону наискорейшего изменения целевой функции в сторону наискорейшего убывания целевой функции