F(x1, x2,...xm) const 4 страница

в списке нет правильного ответа

Вектор градиента - это

вектор, состоящий из первых частных производных целевой функции вектор, позволяющий определить направление убывания функции вектор, состоящий из вторых частных производных целевой функции

в списке нет правильного ответа

Из перечисленных методов какой НЕ относится в методам многомерной оптимизации

Рунге-Кутты

НСЧ ГДШ НСА

Линия уровня - это

множество точек, для которых целевая функция f(x1,x2) принимает постоянное значение

последовательность точек , получаемых методом спуска в списке нет правильного ответа

последовательность значений целевой функции, получаемых методом спуска

Количество итераций, необходимых для того чтобы обеспечить заданную точность по методу дихотомии при решении задачи одномерной оптимизации, если , равно

нет правильного ответа

2

3

Величина шага спуска в аналитическом методе наискорейшего спуска при решении задачи многомерной оптимизации выбирается из условия

в списке нет правильного ответа

На каждой итерации в методе ГДШ при решении задачи многомерной оптимизации шаг уменьшается

в 1000 раз в 3 раза

в 2 раза

в 31 раз

За начальное значение шага ( ) в методе ГДШ при решении задачи многомерной оптимизации принимается

>0

<(b-a)/2

0< <1

<0

Модуль вектора антиградиента в точке минимума равен

0

в списке нет правильного ответа

1

-1

К методам многомерной оптимизации относится метод

Гаусса Симпсона наискорейшего спуска Рунге-Кутта

Вектор первых частных производных целевой функции - это

градиент совокупность точек, для которых

в списке нет правильного ответа

прямая, соединяющая точки с одинаковыми значениями целевой функции

Точкой стационарности называется точка, в которой

матрица вторых производных равна нулю градиент функции отрицателен

матрица вторых производных отрицательно определена

градиент функции равен нулю

Матрица называется

матрица братьев Вачовски матрица Грама матрица Гессе

матрица элементарных исходов

Из перечисленных понятий не относится к методам многомерной оптимизации

правило Рунге безусловная оптимизация матрица Гессе

критерий Сильвестра

Чтобы повысить точность определения точки минимума в методах многомерной оптимизации надо

увеличить количество итераций по поиску минимума

выбрать начальное приближение как можно ближе к точке минимума уменьшить допустимую погрешность

в списке нет правильного ответа

Если на значения параметров оптимизации существуют ограничения, то задача оптимизации называется

векторной условной ограниченной сложной

Модуль (длина) вектора градиента указывает на

направление убывания функции направление возрастания функции

скорость возрастания функции

скорость убывания функции

Достаточное условия минимума заключаются в том, что -:вторые производные функции равны 0

первые производные функции равны 0

угловые миноры матрицы Гессе функции положительны частные производные функции равны 0

Точкой минимума функции является точка

(1;-3/8) (1/2;1)

(-3/5;1) (3/5;-0.2)

Методы спуска при решении задачи многомерной оптимизации – это такие методы, в которых на каждой итерации выполняется условие

<

>

Величину на каждой итерации при решении задачи многомерной оптимизации находят так, чтобы выполнялось условие

В градиентном методе с дроблением шага при решении задачи многомерной оптимизации

Начальная точка при решении задачи многомерной оптимизации выбирается

на линии уровня

из области существования функции на поверхности уровня

в списке нет правильного ответа

Вектор первых частных производных целевой функции - это

в списке нет правильного ответа

прямая, соединяющая точки с одинаковыми значениями целевой функции градиент

совокупность точек, для которых

По количеству параметров задачи оптимизации делятся на

одномерные и многомерные никак не делятся

дискретные и непрерывные одномерные и дискретные

Группа методов, в которых точка минимума (максимума) функции находится путем получения вложенных отрезков, называется

в списке нет правильного ответа методами одномерного поиска методами спуска

градиентными методами

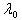В методе ГДШ при решении задачи многомерной оптимизации начальный шаг в большинстве случаев берется равным

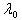
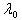=0.5

=0

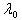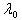=0.1

=1

Длина интервала неопределенности после 3 итерации по методу золотого сечения при решении задачи одномерной оптимизации, если , равна

0.617934

1

0.381924

Погрешность, обусловленная выполнением действий над данными, полученными с ограниченной точностью, это

погрешность метода

в списке нет правильного ответа погрешность округления неустранимая погрешность

На этапе уточнения корней нелинейных уравнений определяют

значение корня с заданной степенью точности значение функции, соответствующее корню уравнения отрезок, содержащий единственный корень совокупность корней уравнения

Процесс решения нелинейного уравнения состоит из

трех этапов двух этапов четырех этапов семи этапов

Правилом выбора неподвижной точки при решении нелинейного уравнения метода хорд является

в списке нет правильного ответа

За начальное приближения при решении нелинейного уравнения методом итераций принимают

, если

, если

в списке нет правильного ответа

Необходимым условием существования корня нелинейного уравненения на отрезке [a;b] является

y XG4Wm0XiJ3G6ASKKwr/e5omfbqP5ZTEr8ryIJiIaUZa8R3P/nwcHq2xFOeWe0fUub/XAz9b9xsDN g1qA+fDgxsTd9Bw4nMCHWRTh+iL7QvJCX3AljUFhB/nWF77ivrCI08cfQuyc2BVmc0gL/Hyefwa/ 9YVX9QV3eoCTmOsg46kRj3qPxyA/Ptuu/wUAAP//AwBQSwMEFAAGAAgAAAAhAOemoT/dAAAABwEA AA8AAABkcnMvZG93bnJldi54bWxMj0FLw0AUhO+C/2F5gje7SYOtxryUUtRTEWwF8faavCah2d2Q 3Sbpv/d5ssdhhplvstVkWjVw7xtnEeJZBIpt4crGVghf+7eHJ1A+kC2pdZYRLuxhld/eZJSWbrSf POxCpaTE+pQQ6hC6VGtf1GzIz1zHVryj6w0FkX2ly55GKTetnkfRQhtqrCzU1PGm5uK0OxuE95HG dRK/DtvTcXP52T9+fG9jRry/m9YvoAJP4T8Mf/iCDrkwHdzZll61CItl8ixRBHkk9lLWQB0Q5kkE Os/0NX/+CwAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAA AABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAA AAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAJlkCRhXAwAAIwsAAA4AAAAAAAAA AAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAOemoT/dAAAABwEAAA8AAAAA AAAAAAAAAAAAsQUAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAAC7BgAAAAA= ">

Метод половинного деления при решении нелинейного уравнения всегда находит корень уравнения f(x)=0, если

корень совпадает с одной из границ отрезка

выполнено условие существования и единственности корня на отрезке в списке нет правильного ответа

корень находится в середине отрезка

Корень нелинейного уравнения f(x)=0 - это

значение переменной х, обращающее уравнение в тождество значение х, при котором функция принимает максимальное значение значение х, при котором функция существует

значение х, при котором функция принимает минимальное значение

Ф-ия сходится к корня, если

Чтобы выбрать x0 в качестве начального приближения при решении нелинейных уравнений в методе Ньютона, необходимо, чтобы в этой точке

функция и вторая производная имели одинаковые знаки функция и первая производная имели одинаковые знаки первая и вторая производная имели одинаковые знаки функция и первая производная имели разные знаки

Метод решения нелинейного уравнения, который требует более близкого к корню начального значения это

метод Ньютона метод итерации метод хорд

в списке нет правильного ответа метод половинного деления

При решении нелинейного уравнения целесообразно выбирать отрезок, на котором отделен корень, небольшой длины в методе

метод хорд касательных метод Ньютона метод итерации

Метод решения нелинейного уравнения, в результате которого получается последовательность вложенных отрезков это

метод половинного деления метод хорд

в списке нет правильного ответа метод Ньютона

метод итерации

Условием окончания процесса итерации при решении нелинейного уравнения по методу хорд служит выражение

Первым приближением к корню, отделенному на отрезке [a;b], при решении нелинейного уравнения методом половинного деления служит

К методам уточнения корней нелинейных уравнений не относится метод итераций

метод хорд

метод половинного деления графический метод

К способам улучшения сходимости метода простой итерации при решении нелинейного уравнения не относятся

в списке нет правильного ответа переход к обратной функции

ввод поправочного коэффициента увеличение количества итераций

В процессе решения уравнения методом простой итерации приближение к корню может осуществляться

только монотонно со стороны начального приближения в списке нет правильного ответа