F(x1, x2,...xm) const 5 страница

только колебательно справа и слева от корня

монотонно или колебательно

За неподвижный конец отрезка [a;b] в методе хорд при решении нелинейного уравнения выбирают конец отрезка, для которого

в списке нет правильного ответа

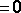Термин - «метод расходится» при решении нелинейного уравнения означает

очередное приближение приближается к корню очередное приближение отдаляется от корня

в списке нет правильного ответа

очередное приближение равно предыдущему значению

К методам отделения корней нелинейных уравнений не относится

графический аналитический метод табличный метод метод итераций

Утверждение, что численный метод решения нелинейных уравнений «сходится», означает, что

в списке нет правильного ответа очередное приближение отдаляется от корня очередное приближение приближается к корню

очередное приближение равно предыдущему значению приближения

При решении нелинейного уравнения малая скорость сходимости характерна для метода

хорд

Ньютона половинного деления простой итерации

Принцип графического отделения корня, основанного на графическом способе решения, заключается в

нахождение максимума и минимума

отыскании тотрезком, на которых функция имеет пересечение с осю ОХ отыскание точек, в которых функция пересекает ось ОУ отыскания промежутка [a;b]

Метод хорд при решении нелинейного уравнения позволяет вычислить отделенный корень с заданной погрешностью если

на отрезке один корень

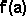в списке нет правильного ответа правильно выбран неподвижный конец отрезка

выполняется условие

Уточнить корень уравнения графическим методом

можно нельзя

в списке нет правильного ответа

можно, если функция несложная

При отделении корней нелинейных уравнений критическими точками считаются

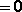
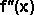
в списке нет правильного ответа

Если на заданном отрезке имеется два корня, то при решении нелинейного уравнения о методе итераций можно сказать

метод обеспечит сходимость к одному из корней метод разойдется

сходимость метода не гарантирована в списке нет правильного ответа

Метод решения нелинейного уравнения сходится, если

за конечное число итераций корень найден с заданной точностью метод позволяет найти точное значение корня

каждое очередное приближение к корню принадлежит отделенному отрезку от итерации к итерации происходит увеличение значения функции

Отделение корней нелинейного уравнения сводится к нахождению отрезков, в пределах которых функция

не монотонна и изменяет свой знак монотонна и изменяет свой знак не монотонна

Глобальный минимум является

первым по порядку из локальных наименьшим из локальных наибольшим из локальных

в списке нет правильного ответа

Необходимым условием существования экстремума функции F(x) на отрезке [a;b] является

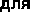
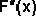
в списке нет правильного ответа

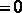
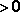
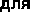
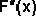
В методе дихотомии при решении задачи одномерной оптимизации на каждой итерации отрезок неопределенности уменьшается

в несколько раз почти в 2 раза

в 1.618 раз

в списке нет правильного ответа

В методах одномерной оптимизации при переходе к следующей итерации часть отрезка [a;b]

можно отбросить, потому что

на отрезке [a;b] целевая функция унимодальная в отброшенной части функция возрастает потому что производная монотонно возрастает

отбрасывается часть отрезка, содержащего большие значения функции

В методах одномерной оптимизации при переходе к следующей итерации часть отрезка можно отбросить, считая, что там нет минимума функции, потому что

функция на отрезке неопределенности унимодальна в списке нет правильного ответа

правильно выбран параметр метода

на каждой итерации выбирают меньшее значение функции

При решении задачи одномерной оптимизации более высокой скоростью сходимости обладает метод прямого перебора

метод дихотомии

в списке нет правильного ответа метод золотого сечения

Метод одномерной оптимизации, требующий проведения меньшего количества итераций для достижения заданной точности результата - это

метод дихотомии метод золотого сечения метод прямого перебора

К группе методов одномерного поиска относится

метод Симпсона метод Ньютона метод Вегстейна

в списке нет правильного ответа метод дихотомии

Чтобы повысить точность метода дихотомии при решении задачи одномерной оптимизации надо

в списке нет правильного ответа увеличить отрезок неопределенности уменьшить заданную погрешность уменьшить количество итераций

На скорость сходимости метода дихотомии при решении задачи одномерной оптимизации вид функции

чем круче функция, тем быстрей сходимость в списке нет правильного ответа

для пологих функций сходимость ниже

не влияет

Чтобы повысить точность метода прямого перебора при решении задачи одномерной оптимизации надо

задать меньшее значение погрешности увеличить шаг перебора

в списке нет правильного ответа

сократить отрезок неопределенности

Чтобы повысить точность метода золотого сечения при решении задачи одномерной оптимизации необходимо

задать меньшее значение погрешности уменьшить шаг перебора

в списке нет правильного ответа сократить отрезок неопределенности

Наименьшее значение функции в некоторой окрестности - это

нет правильного ответа глобальный минимум оптимальное значение локальный минимум

Значения функции (при использовании метода золотого сечения) в точках первой итерации равны

0.382; 0.146

0.456; 0.258

1.256; 0.849

0.168; 0.387

Значения функции (при использовании метода золотого сечения) в точках равны

2.618; 1.910

1,365; 0,695

3.254; 2.439

0.256; 0.512

Отрезок неопределенности для функции равен

[2;3]

[-5;-4]

нет правильного ответа

[-9;-8]

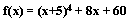Функция имеет минимум на отрезке

[4;5]

[-10;-9] [-7;-5] [1;2]

Группа методов, где на каждой итерации интервал неопределенности уменьшается и стягивается к точке минимума - это методы

Рунге-Кутта одномерного поиска Ньютона

итерации

Задача нахождения максимума целевой функции сводится к задаче

без замены функции замены f(x) на f(-x) замены f(x) на –f(x)

если количество независимых переменных n=1 при решении задачи одномерной оптимизации , то это

одномерная оптимизация многомерная оптимизация

в списке нет правильного ответа

Длина интервала неопределенности по методу дихотомии при решении задачи одномерной оптимизации после двух итераций, если равна

нет правильного ответа

0.5

1

Методы одномерного поиска применяются для

гладких функций постоянных функций

унимодальных функций

Золотым сечением при решении задачи одномерной оптимизации называется такое деление отрезка на две неравные части, при котором

нет верного ответа

отношение длины всего отрезка к длине его большей части равно отношению длины большей части отрезка к длине его меньшей части

отношение длины всего отрезка к длине его меньшей части равно отношению длины большей части отрезка к длине его меньшей части

отношение длины всего отрезка к длине его большей части не равно отношению длины большей части отрезка к длине его меньшей части

Точки второй итерации на отрезке [0;2], если даны значения функций первой итерации

равны

(по методу дихотомии при решении задачи одномерной оптимизации),

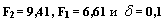
[1.65;0.36] [5.28;3.69] [0.33;0.68]

[0.45;0.65]

Наименьшее значение функции в некоторой окрестности - это

глобальный минимум оптимальное значение нет правильного ответа локальный минимум

Метод оптимизации, при котором на каждой итерации вычисляется только одно значение целевой функции, это

в списке нет правильного ответа метод дихотомии

все перечисленные методы

метод Ньютона метод золотого сечения

Метод одномерной оптимизации, где проводится большее количество вычислений функции для достижения необходимой точности - это метод

нет правильного ответа

Эйлера золотого сечения дихотомии

k+1-й отрезок неопределенности в методе дихотомии при решении задачи одномерной оптимизации находят по правилу

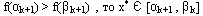
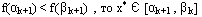
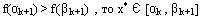
Точки второй итерации на отрезке [1;2], если даны значения функции после первой итерации

(по методу дихотомии при решении задачи одномерной оптимизации)

равны

[0.2;0.5] [4.5;3.2] [1.6; 2.5]

[1.2;1.4]

К методам одномерного поиска относятся метод

градиентного спуска сканирования золотого сечения дихотомии

Количество итераций, необходимых для того чтобы обеспечить заданную точность по методу дихотомии при решении задачи одномерной оптимизации, если , равно

4

3

нет правильного ответа

Метод одномерной оптимизации, где длину конечного интервала неопределенности вычисляют по следующей формуле - это метод

золотого сечения дихотомии

нет правильного ответа прямого перебора

Точность метода прямого перебора при решении задачи одномерной оптимизации повышается, если

увеличить шаг перебора нет правильного ответа

увеличить отрезок неопределенности

Если поменять у целевой функции знак на противоположный, то с помощью методов одномерной оптимизации можно найти

в списке нет правильного ответа максимум функции выпуклость функции минимум функции

Методы одномерного поиска при решении задачи одномерной оптимизации применяются для функций