Необходимое условие экстремума функции

Определение 4. Точка называется точкой локального минимума функции , если для всех значений , достаточно близких к и не равных , выполняется условие .

Определение 5. Точка называется точкой локального максимума функции , если для всех значений , достаточно близких к и не равных , выполняется условие .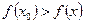

Определение 6. Точка называется точкой экстремума функции , если она является точкой минимума или точкой максимума.

Теорема 2 (необходимое условие экстремума функции). Если точка является точкой экстремума функции и значение 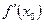определено, то .

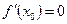Замечание. Может оказаться, что в точке экстремума производная 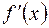не определена.

Определение 6. Точка называется критической точкой первого рода функции , если 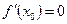или значение 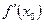не определено.

Замечание. В критической точке первого рода функция может иметь экстремум, но не обязательно.