Исследование функции на асимптоты графика

Теорема 1. Если – точка разрыва второго рода функции , то есть , то прямая является асимптотой кривой .

Теорема 2. Если существуют конечные пределы и , то прямая является асимптотой кривой .

Замечание. Прямая называется вертикальной асимптотой, так как она перпендикулярна оси абсцисс. В отличие от нее прямая называется наклонной асимптотой. Если , то прямая параллельна оси ординат, поэтому такую асимптоту можно назвать горизонтальной.

Пример. Найти асимптоты кривой .

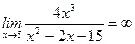Решение. Так как при и , а при этих значениях, то и , то есть точки и являются точками разрыва второго рода данной функции, поэтому прямые и являются вертикальными асимптотами ее графика.

Так как существуют конечные пределы

и

, то прямая является наклонной асимптотой графика данной функции.

Ответ: прямые , , -- асимптоты графика функции.