
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для приближенных вычислений
Определение. Дифференциалом функции  в точке
в точке  называется произведение
называется произведение 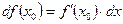 , где
, где  ‒ приращение аргумента.
‒ приращение аргумента.
Теорема. Если  , то при малых значениях приращения
, то при малых значениях приращения  аргумента функции ее дифференциал является главной частью ее приращения.
аргумента функции ее дифференциал является главной частью ее приращения.
По определению производной  .
.
По определению предела функции из этого равенства следует, что 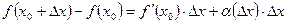 , где
, где  -- бесконечно малая функция при
-- бесконечно малая функция при  , то есть
, то есть  .
.
Если  , то
, то  .
.
Это значит, что при малых значениях  слагаемое
слагаемое  пренебрежимо мало в сравнении со слагаемым
пренебрежимо мало в сравнении со слагаемым  , то есть можно считать, что
, то есть можно считать, что  , или
, или  .
.
Теорема доказана.
Замечание. Из равенства  получаем:
получаем:
 .
.
Эту формулу используют для приближенных вычислений значений функции. На практике ее удобнее представить в виде
 ,
,
где выражение  и значение
и значение  определяются условием задания, а значение
определяются условием задания, а значение  выбирается произвольно с учетом двух условий: во-первых,
выбирается произвольно с учетом двух условий: во-первых,  должно как можно меньше отличаться от
должно как можно меньше отличаться от  , во-вторых, значения
, во-вторых, значения  и
и 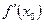 должны легко вычисляться без таблиц или калькулятора.
должны легко вычисляться без таблиц или калькулятора.
Пример. Вычислить приближенно  .
.
Решение


 ,
, 

 .
.
Пусть  . Тогда
. Тогда  ,
,
 ,
,
 .
.
Ответ: 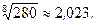
Для сравнения: вычисления на микрокалькуляторе дают результат 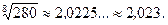
Дата добавления: 2015-04-18; просмотров: 257; Мы поможем в написании вашей работы!; Нарушение авторских прав |