Уравнение касательной к графику функции

Теорема. Уравнение касательной к кривой 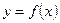в ее точке имеет вид .

Пример. Составить уравнение касательной к кривой в точке .

Решение: Уравнение касательной к кривой 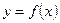в ее точке имеет вид .

Из условия следует, что , .

Тогда ,

,

Уравнение касательной имеет вид , или .

Ответ: .

Дифференциал функции.

Геометрический смысл дифференциала

Определение. Дифференциалом функции в точке называется произведени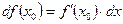е , где ‒ приращение аргумента.

Пример. Найти , если .

Решение. По определению дифференциала, .

Так как , то

.

Тогда

Ответ: .

Теорема о геометрическом смысле дифференциала. Дифференциал функции в точке численно равен приращению ординаты точки касательной к кривой 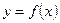в ее точке , соответствующему приращению аргумента функции (см. рис. 1 стр. 11).

Применение дифференциала функции