
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Достаточные условия монотонности функции
Определение 1. Функция называется возрастающей на данном промежутке, если для любых двух значений аргумента, взятых из этого промежутка, большему значению аргумента соответствует большее значение функции.
Определение 2. Функция называется убывающей на данном промежутке, если для любых двух значений аргумента, взятых из этого промежутка, большему значению аргумента соответствует меньшее значение функции.
Определение 3. Функция называется постоянной на данном промежутке, если для любого значения аргумента, взятого из этого промежутка, функция принимает одно и то же значение.
Теорема 1 (достаточное условие монотонности функции).
Пусть функция  имеет на интервале
имеет на интервале 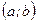 производную
производную 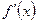 . Тогда:
. Тогда:
если  при любом значении
при любом значении 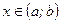 , то
, то  возрастает на интервале
возрастает на интервале 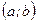 ;
;
если  при любом значении
при любом значении 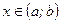 , то
, то  убывает на интервале
убывает на интервале 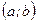 ;
;
если  при любом значении
при любом значении 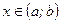 , то
, то  является постоянной на интервале
является постоянной на интервале 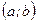 .
.
Дата добавления: 2015-04-18; просмотров: 277; Мы поможем в написании вашей работы!; Нарушение авторских прав |