На выпуклость и точки перегиба графика

Определение 1. График функции называется выпуклым вверх (или просто выпуклым) на данном интервале, если касательная к нему в каждой его точке расположена выше графика. График функции называется выпуклым вниз (или вогнутым) на данном интервале, если касательная к нему в каждой его точке расположена ниже графика.

Определение 2. Точка графика функции называется точкой перегиба графика, если по одну сторону от этой точки график является выпуклым вверх, а по другую сторону выпуклым вниз.

Теорема 1 (достаточные условия выпуклости графика).

Пусть функция имеет на интервале 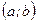производную 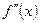. Тогда:

если 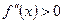при любом значении 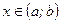, то график функции является выпуклым вниз на интервале ;

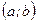если 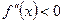при любом значении 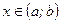, то график функции является выпуклым вверх на интервале .

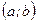Замечание. Если 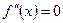при любом значении 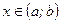, то является линейной функцией на интервале 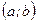, то есть ее график является прямой линией или ее частью (отрезком, лучом). Выпуклым он в этом случае не называется.

Теорема 2 (достаточное условие перегиба графика).

Пусть функция имеет на интервале 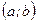непрерывные производные 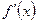и 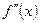. Тогда:

если при переходе через точку вторая производная 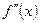меняет знак, то ‒ абсцисса точки перегиба графика;

если при переходе через точку вторая производная 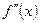не меняет знак, то в точке перегиба у графика нет.