Неопределенный интеграл, его свойства

Определение 2. Множество всех первообразных функции на данном интервале называется неопределённым интегралом от функции на этом интервале.

Согласно теореме о множестве первообразных данной функции,

,

где – одна из первообразных функции , С – произвольная постоянная (она называется постоянной интегрирования).

Теорема (достаточное условие интегрируемости функции).

Если функция непрерывна на интервале , то существует интеграл 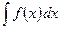на интервале .

Свойства неопределенного интеграла

1°. .

2°. .

3°. , если

4°. .

Формулы интегрирования

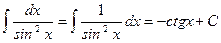
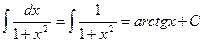
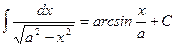
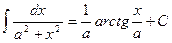
Методы вычисления неопределенных интегралов.

Непосредственное интегрирование

Непосредственным интегрированием называют такой метод вычисления неопределенного интеграла, при котором данный интеграл сводят к алгебраической сумме табличных интегралов путем преобразования подынтегральной функции и применения свойств 3° и 4°.

Пример