Геометрический смысл определенного интеграла

Определение 1. Пусть функция непрерывна и принимает неотрицательные значения на отрезке . Фигура, ограниченная графиком функции , осью абсцисс и прямыми , называется криволинейной трапецией.

Определение 2. Пусть дана криволинейная трапеция, ограниченная графиком функции , осью абсцисс и прямыми .

Разделим отрезок на n частей (не обязательно равных), длины этих частей обозначим 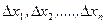. На каждом из полученных отрезков возьмём произвольную точку. Эти точки обозначим

На каждом частичном отрезке как на основании построим прямоугольник, высота которого равна значению функции в точке, выбранной на этом отрезке.

Фигура, составленная из n построенных прямоугольников, называется ступенчатой фигурой.

Площадь ступенчатой фигуры равна сумме площадей прямоугольников, составляющих эту фигуру, то есть

.

Замечание. Площадь ступенчатой фигуры зависит и от числа n разбиений отрезка на части, и от выбора точек на частичных отрезках. Но чем больше значение n, тем меньше площадь ступенчатой фигуры отличается от площади S криволинейной трапеции.

Пусть теперь число n разбиений отрезка стремится к бесконечности так, что длина каждого частичного отрезка стремится к нулю. Можно доказать, что для непрерывной функции f(x) предел последовательности площадей ступенчатых фигур при существует и не зависит ни от способа разбиения отрезка на части, ни от выбора точек на частичных отрезках. Этот предел и называют площадью криволинейной трапеции.

Определение 3. Площадью криволинейной трапеции называется предел последовательности площадей ступенчатых фигур при условии, что число n разбиений отрезка стремится к бесконечности так, что длина каждого частичного отрезка стремится к нулю.

Теорема о геометрическом смысле определённого интеграла.Если функция непрерывна и неотрицательна на отрезке , то определённый интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции , осью абсцисс и прямыми : .