
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
С разделяющимися переменными
Дифференциальным уравнением первого порядка с разделяющимися переменными называется уравнение вида 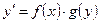 , где
, где  и
и 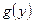 – данные функции,
– данные функции,  – искомая функция.
– искомая функция.
Алгоритм решения такого уравнения рассмотрим на конкретном примере.
Пример 1. Найти общее решение дифференциального уравнения 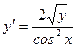 .
.
Решение:
1) Заменить производную искомой функции отношением дифференциалов  :
:  .
.
2) Разделить переменные (то есть представить уравнение в таком виде, чтобы в одной его части содержалось выражение только от x и dx, а в другой части – выражение только от y и dy): 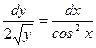 .
.
3) Проинтегрировать каждую часть уравнения по соответствующей переменной: 

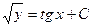 .
.
4) Решить полученное уравнение относительно y: 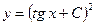 .
.
Ответ: 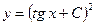 .
.
Пример 2. Найти частное решение дифференциального уравнения  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 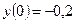 .
.
Решение:
1. Находим общее решение уравнения:
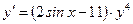

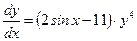



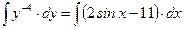

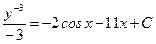



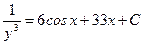

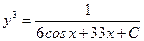

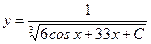 .
.
2. Используя начальное условие, находим значение C:
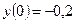









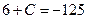

 .
.
3. Подставляя найденное значение  в общее решение
в общее решение 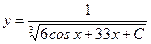 , получаем искомое частное решение
, получаем искомое частное решение 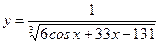 .
.
Ответ: 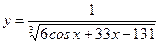 .
.
Дата добавления: 2015-04-18; просмотров: 243; Мы поможем в написании вашей работы!; Нарушение авторских прав |