
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аналоги практических заданий к экзамену по математике
Задание 1. Вычислить предел  .
.
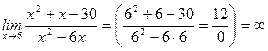 .
.
Задание 2. Вычислить предел 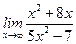 .
.
 .
.
Задание 3. Вычислить предел 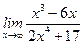 .
.
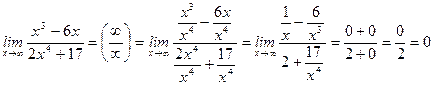 .
.
Задание 4. Вычислить предел 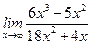 .
.
 .
.
Задание 5. Вычислить предел 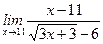 .
.
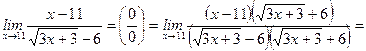
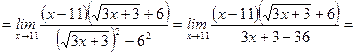
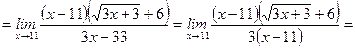
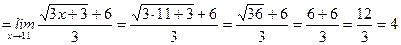 .
.
Задание 6. Вычислить предел 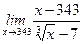 .
.
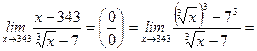
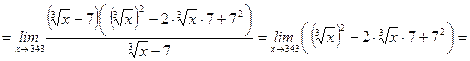
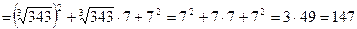 .
.
Задание 7. Вычислить предел 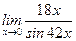 .
.
 .
.
Использован замечательный предел 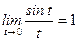 при
при 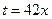 .
.
Задание 8. Вычислить предел 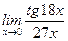 .
.
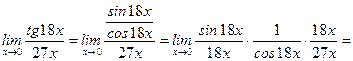

 .
.
Использован замечательный предел 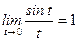 при
при 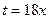 .
.
Задание 9. Вычислить предел  .
.

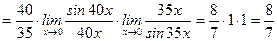 .
.
Использован замечательный предел 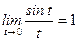 при
при 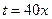
и при 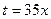 .
.
Задание 10. Вычислить предел  .
.

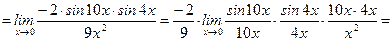
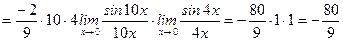 .
.
Использованы формула 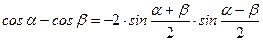 при
при 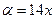 ,
, 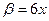 и замечательный предел
и замечательный предел 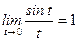 при
при  и
и 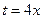 .
.
Задание 11. Вычислить предел: 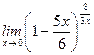 .
.
 .
.
Использован замечательный предел  при
при  .
.
Задание 12. Вычислить предел: 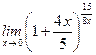 .
.
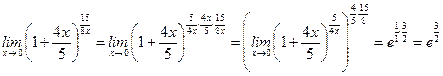 .
.
Использован замечательный предел  при
при  .
.
Задание 13. Вычислить предел:  .
.
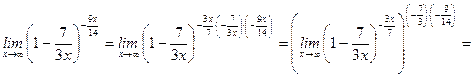
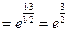 .
.
Использован замечательный предел 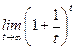 при
при 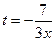 .
.
Задание 14. Исследовать на непрерывность функцию
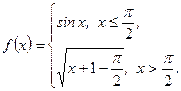
Решение. Функция  непрерывна на промежутках
непрерывна на промежутках 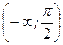 и
и 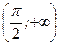 , так как совпадает на этих промежутках соответственно с непрерывными функциями
, так как совпадает на этих промежутках соответственно с непрерывными функциями 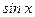 и
и 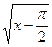 . Точкой разрыва может быт Решение. Функция
. Точкой разрыва может быт Решение. Функция  непрерывна на промежутках
непрерывна на промежутках 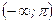 и
и 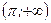 , так как совпадает на этих промежутках соответственно с непрерывными функциями
, так как совпадает на этих промежутках соответственно с непрерывными функциями 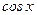 и
и 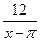 . Точкой разрыва может быть только точка
. Точкой разрыва может быть только точка 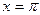 .
.
Так как 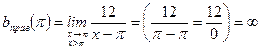 , то точка
, то точка 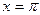 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Ответ: данная функция непрерывна на промежутках 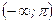 и
и 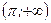 ; точка
; точка 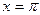 является точкой разрыва второго рода.
является точкой разрыва второго рода.
ь только точка  .
.
 ,
,  ,
,
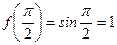 .
.
Так как  , то в точке
, то в точке  функция
функция  непрерывна.
непрерывна.
Ответ: данная функция непрерывна на промежутке 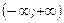 .
.
Задание 15. Исследовать на непрерывность функцию
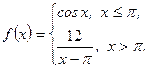
Решение. Функция  непрерывна на промежутках
непрерывна на промежутках 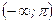 и
и 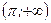 , так как совпадает на этих промежутках соответственно с непрерывными функциями
, так как совпадает на этих промежутках соответственно с непрерывными функциями 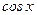 и
и 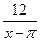 . Точкой разрыва может быть только точка
. Точкой разрыва может быть только точка 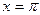 .
.
Так как 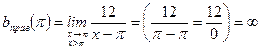 , то точка
, то точка 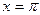 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Ответ: данная функция непрерывна на промежутках 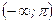 и
и 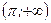 ; точка
; точка 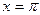 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Задание 16. Исследовать на непрерывность функцию

Решение. Функции  и
и  непрерывны на промежутке
непрерывны на промежутке 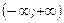 ,
, 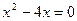 при
при 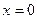 и при
и при 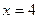 , поэтому функция
, поэтому функция  непрерывна на промежутках
непрерывна на промежутках 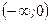 ,
, 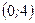 и
и 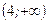 .
.
Точки 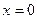 и
и 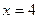 являются точками разрыва, так как в этих точках функция
являются точками разрыва, так как в этих точках функция  не определена. Определим тип разрыва в каждой из них.
не определена. Определим тип разрыва в каждой из них.
Так как 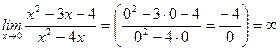 , то точка
, то точка 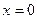 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Та как 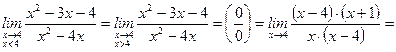
 , то есть
, то есть  и
и 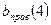 конечные и равные, то точка
конечные и равные, то точка 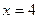 является точкой устранимого разрыва.
является точкой устранимого разрыва.
Ответ: данная функция непрерывна на промежутках 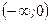 ,
, 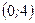 и
и 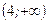 ;
; 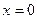 ‒ точка разрыва второго рода,
‒ точка разрыва второго рода, 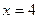 ‒ точка устранимого разрыва.
‒ точка устранимого разрыва.
Задание 17. Составить уравнения асимптот кривой  .
.
Решение. Так как 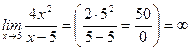 , то есть точка
, то есть точка 
является точкой разрыва второго рода функции 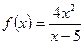 ,то прямая
,то прямая  является вертикальной асимптотой данной кривой.
является вертикальной асимптотой данной кривой.
Так как существуют конечные пределы
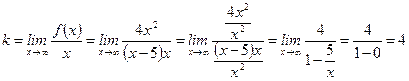 и
и 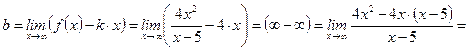
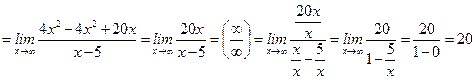 ,
,
то прямая 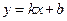 , то есть
, то есть 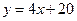 , является наклонной асимптотой данной кривой.
, является наклонной асимптотой данной кривой.
Ответ: асимптотами данной кривой являются прямые  и
и 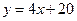 .
.
Задание 18. Вычислить 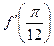 , если
, если 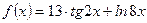 .
.
Решение

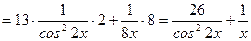

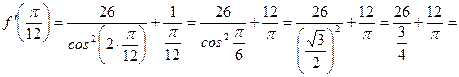
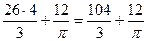
Ответ: 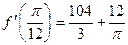 .
.
Задание 19. Вычислить  , если
, если 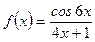 .
.
Задание 20. Вычислить 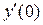 , если
, если 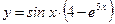 .
.
Дата добавления: 2015-04-18; просмотров: 217; Мы поможем в написании вашей работы!; Нарушение авторских прав |