Второго порядка с постоянными коэффициентами

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами – это уравнения вида

(*)

где – искомая функция, a, b, c – действительные числа.

Общее решение такого уравнения можно найти, используя приведенный ниже алгоритм.

1. На множестве комплексных чисел найти корн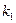и и характеристического уравнения данного дифференциального уравнения

.

2. Записать общее решение уравнения (*) в одном из видов:

а) если 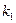и – действительные числа и , то ;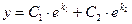

б) если 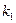и – действительные числа и , то ;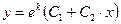

в) есл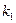и и – комплексные числа вида , то ;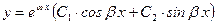

Пример 1. Найти общее решение дифференциального уравнения .

Решение

1) На множестве комплексных чисел найдем корни уравнения

.

Используя формулу 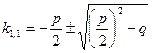, получаем ,

2) по пункту 2в алгоритма при , получаем общее решение дифференциального уравнения в виде

Ответ: .

Пример 2. Найти общее решение дифференциального уравнения .

Решение

1) На множестве комплексных чисел найдем корни уравнения

.

,

2) по пункту 2в алгоритма при , получаем общее решение дифференциального уравнения в виде

Ответ: .