Логические высказывания.

Основные логические операции над высказываниями, их свойства

Определение 1. Высказыванием называется утверждение, о котором можно однозначно судить, истинно оно или ложно.

Высказывания будем обозначать большими латинскими буквами. Содержание высказывания будем записывать в кавычках или в круглых скобках.

Примеры.

A = «Дважды два – четыре»; B = (Сегодня первое октября)

Определение 2. Отрицанием (инверсией) данного высказывания 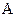называется высказывание 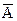, определяемое следующей таблицей истинности:

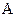
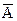
Определение 3. Дизъюнкцией (логической суммой) данных высказывани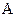й и 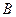называется высказывание 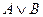, определяемое следующей таблицей истинности:

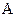
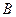
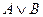
Определение4. Конъюнкцией (логическим произведением) данных высказывани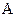й и 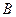называется высказывание 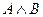, определяемое следующей таблицей истинности:

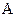
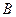
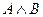
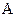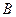Определение 5. Импликацией данных высказываний и называется высказывание , определяемое следующей таблицей истинности:

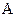
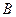
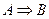
Определение 6. Эквиваленцией данных высказывани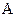й и 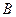называется высказывание 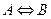, определяемое следующей таблицей истинности:

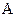
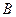
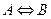
Пример. Составить таблицу истинности высказывания .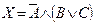

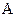
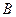
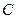
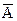
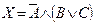
Пример. Установить, равносильны ли высказывания 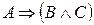и .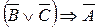

Составим таблицу истинности этих высказываний.

A	B	C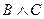

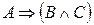
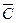
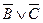
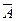
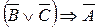
Сравнивая значения высказывани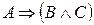й и 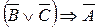, убеждаемся в их равносильности.