Способы задания функции

1. Аналитический способ задания функции.

Функция задается уравнением вида , где 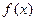– выражение с переменной x. Это уравнение позволяет по заданному значению аргумента найти соответствующее значение функции.

Примеры: , , .

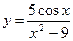Замечание 1. При аналитическом задании функции естественной областью определения функции называется множество всех значений аргумента, для которых определено данное выражение с переменной.

Замечание 2. Одно и то же уравнение , рассматриваемое на разных множествах, задает разные функции, свойства которых могут существенно различаться. Поэтому при задании функции, кроме аналитического выражения, указывают и область определения функции. Если же в условии область определения не задана, то по умолчанию рассматривают естественную, то есть максимально возможную, область определения функции.

2. Графический способ задания функции.

Определение 2. Графиком функции называется множество точек координатной плоскости, абсциссы которых являются значениями аргумента, а ординаты – соответствующими значениями функции.

График функции очень наглядно представляет ее основные свойства. Кроме того, не каждую функцию, заданную графически, можно задать и аналитически.

Если график функции уже построен, то по заданному значению аргумента можно найти соответствующее значение функции.

3. Табличный способ задания функции.

Замечание 1. Табличным способом можно задать функцию только в том случае, когда количество значений ее аргумента конечное и не очень большое.

Обычно мы составляем таблицу некоторых значений функции при построении ее графика.

4. Словесный способ задания функции.

В этом случае закон соответствия между элементами данных множеств задается словесным описанием.

Пример. На множестве натуральных чисел задана функция следующим образом: y — количество делителей данного натурального числа x.

Задать эту функцию аналитически нельзя, но можно найти ее значение для любого значения аргумента, например: , , , .