Линейные однородные дифференциальные уравнения

Первого порядка

Однородное линейное дифференциальное уравнение первого порядка имеет вид , где – данная функция, – искомая функция.

Его общее решение можно представить в виде , где – какая-нибудь первообразная функции , C – произвольная константа.

Пример 1. Найти общее решение дифференциального уравнения .

Решение

, где – первообразная функции . Множество всех первообразных функции найдем как неопределенный интеграл:

При 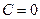получаем 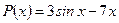, тогда , поэтому .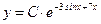

Ответ: .

Пример 2. Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию .

Решение

1. Находим общее решение уравнения:

.

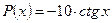
2. Используя начальное условие, находим значение C:

.

3. Подставляя найденное значение в общее решение , получаем искомое частное решение .

Ответ: .