
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Простейшие дифференциальные уравнения второго порядка
Простейшее дифференциальное уравнение первого порядка имеет вид 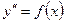 , где
, где  – данная функция,
– данная функция,  – искомая функция.
– искомая функция.
Общее решение уравнения можно найти, дважды проинтегрировав правую часть уравнения: 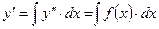 ,
, 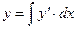 . Общее решение уравнения имеет вид
. Общее решение уравнения имеет вид 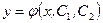 , то есть содержит две произвольные постоянные
, то есть содержит две произвольные постоянные 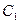 и
и 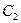 .
.
Давая величинам 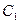 и
и 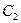 произвольные конкретные значения, из общего решения получают его частные решения.
произвольные конкретные значения, из общего решения получают его частные решения.
Чтобы найти конкретные значения 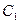 и
и 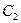 , нужно задать два дополнительных условия.
, нужно задать два дополнительных условия.
Задача Коши для дифференциального уравнения второго порядка состоит в нахождении его частного решения, удовлетворяющего начальным условиям вида  ,
, 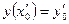 , где
, где  ,
,  и
и 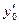 – данные числа.
– данные числа.
Пример 1. Найти общее решение дифференциального уравнения 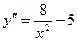 .
.
Решение
1) 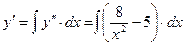

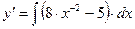

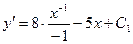

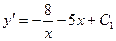 ;
;
2) 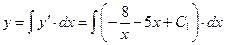

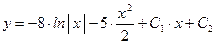 .
.
Ответ: 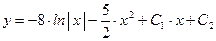 .
.
Пример 2. Найти частное решение дифференциального уравнения 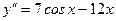 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 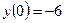 ,
, 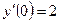 .
.
Решение:
1. Находим общее решение уравнения:
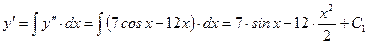

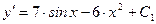 ;
;
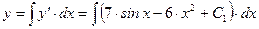

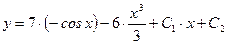

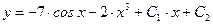 .
.
2. Используя начальные условия, находим значения 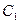 и
и 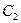 :
:
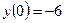

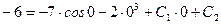

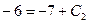

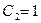 ;
;
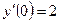

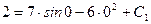

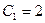 .
.
3. Подставляя найденные значения 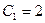 и
и 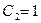 в общее решение
в общее решение 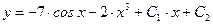 , получаем искомое частное решение
, получаем искомое частное решение 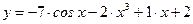 .
.
Ответ: 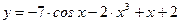 .
.
Дата добавления: 2015-04-18; просмотров: 267; Мы поможем в написании вашей работы!; Нарушение авторских прав |