Задачи, приводящие к дифференциальным уравнениям. Пример 1. Тело движется прямолинейно со скоростью

Пример 1. Тело движется прямолинейно со скоростью 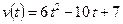. Найти закон движения тела, если к моменту 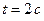тело прошло путь .

Решение.

Закон прямолинейного движения тела имеет вид , где – путь (в метрах), пройденный телом за промежуток времени 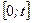от момента 0 секунд до момента секунд.

Согласно физическому смыслу первой производной, 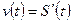, поэтому из условия следует, что , то есть функцию нужно найти из уравнения . (Это уравнение называется дифференциальным уравнением первого порядка).

Получаем: 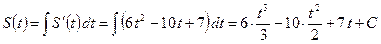, или , где C - постоянная интегрирования, то есть любое число или выражение с любыми переменными, кроме переменной x.

(Полученная функция 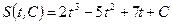называется общим решением данного дифференциального уравнения).

Для нахождения конкретного значения константы C используем условие при 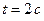, то есть .

Из уравнения получаем:

.

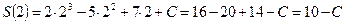Т. к. 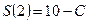и , то 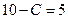, поэтому .

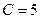Подставив 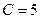в уравнение 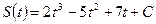, получаем решение данной задачи: 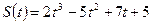. Эта функция называется частным решением данного дифференциального уравнения.

Основные понятия

Определение 1. Дифференциальным уравнением называется уравнение, в котором неизвестной является некоторая функция, при условии, что уравнение содержит хотя бы одну производную искомой функции.

Определение 2. Порядкомдифференциального уравнения называется порядок входящей в это уравнение старшей производной искомой функции.

В общем случае дифференциальное уравнение n-го порядка можно представить в виде , где – искомая функция.

Примеры:

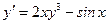– дифференциальное уравнение первого порядка;

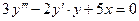– дифференциальное уравнение третьего порядка.

Определение 3. Решениемдифференциального уравнения называется функция, при подстановке которой в уравнение вместо неизвестной функции это уравнение превращается в тождество относительно независимой переменной.

Замечание. Общее решение дифференциального уравнения n-го порядка содержит n произвольных постоянных, то есть имеет вид .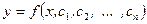

Давая постоянным 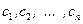различные конкретные значения, из общего решения получают различные частные решения.

Частные решения дифференциального уравнения, которые не получаются из общего решения ни при каких значениях постоянных 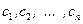, называются особыми решениями дифференциального уравнения.

Определение 4. Интегральной кривойдифференциального уравнения называется график любого его частного решения.

Определение 5. Задача Коши длядифференциального уравнения n-го порядка состоит в нахождении его частного решения 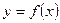, удовлетворяющего условиям 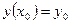, , 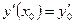, 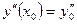… , , 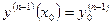где 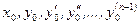– данные числа.

Условия 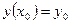, , 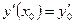, 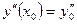… , 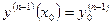называются начальными условиями задачи Коши.