Определенный интеграл, его свойства

Определение 1. Пусть функция определена на отрезке . Разделим этот отрезок на n частей (не обязательно равных). Длины этих частей обозначим 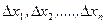. На каждом из полученных отрезков возьмём произвольную точку. Эти точки обозначим (см. рис. 2, стр. 17).

Тогда сумма 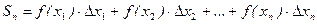называется интегральной суммой для функции f(x) на отрезке .

Определение 2. Если существует предел последовательности интегральных сумм для функции на отрезке при условии, что число n разбиений отрезка стремится к бесконечности так, что длина каждого частичного отрезка стремится к нулю, и если этот предел не зависит ни от способа разбиения отрезка на части, ни от выбора точек на частичных отрезках, то этот предел называется определённым интегралом от функции на отрезке .

Определение 3. Если существует определённый интеграл от функции на отрезке , то функция называется интегрируемой на отрезке .