Основные свойства числовых функций

Определение 3. Функция называется четной, если для любого значения x, взятого из области определения функции, значение тоже принадлежит области определения и выполняется равенство .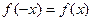

Определение 4. Функция называется нечетной, если для любого значения x, принадлежащего области определения, значение тоже принадлежит области определения и выполняется равенство .

Замечание 1.Если функция является четной, то ее график симметричен (сам себе) относительно оси ординат. Обратное утверждение тоже верно, то есть если график функции симметричен относительно оси ординат, то функция является четной.

Замечание 2.Если функция является нечетной, то ее график симметричен (сам себе) относительно начала координат. Обратное утверждение тоже верно, то есть если график функции симметричен относительно начала координат, то функция является нечетной.

Замечание 3. Существуетединственная функция, являющаяся одновременно четной и нечетной. Это функция . Графиком этой функции является ось абсцисс. Она симметрична (сама себе) и относительно оси ординат и относительно начала координат.

Замечание 4. Функция может не быть ни четной, ни нечетной. В этом случае график ее не является симметричным относительно оси ординат, но может иметь другие оси симметрии. График не является также симметричным относительно начала координат, хотя может иметь другие центры симметрии.

Примеры:

, , — четные функции;

, , — нечетные функции;

, — не четные и не нечетные функции.

Определение 5.Функция называется возрастающей на данном промежутке, если для любых двух значений аргумента, взятых из этого промежутка, большему значению аргумента соответствует и большее значение функции.

Определение 6.Функция называется убывающей наданном промежутке, если для любых двух значений аргумента, взятых из этого промежутка, большему значению аргумента соответствует меньшее значение функции.

Определение 7. Функция называется постоянной на данном промежутке, если для всех значений аргумента, взятых из этого промежутка, функция принимает одно и то же значение.

Определение 8. Функция называется монотонной на данном промежутке, если на этом промежутке она только возрастает, или только убывает, или является постоянной.

Примеры:

Функция возрастает на промежутке .

Функция убывает на промежутках 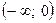и .

Функция , убывает на промежутке 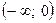и возрастает на промежутке .

Определение 9. Функция f(x) называется ограниченной, если существует такое положительное число m, что для всех значений аргумента х, взятых из области определения, выполняется условие .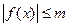

Примеры: функции , , являются ограниченными, так как , , .

Функции , не являются ограниченными, так как принимают значения, большие любого наперед заданного числа m.

Определение 10. Функция называется периодической, если существует число такое, что для любого значения x, взятого из области определения функции, выполняются равенства: и .

Число T называется периодом функции .

Замечание 1. Если число Т является периодом функции , то и любое число Т∙n, n Z, тоже является ее периодом, поэтому обычно указывают наименьший положительный период функции.

Замечание 2. График периодической функции состоит из повторяющихся частей, поэтому достаточно построить график на любом промежутке длиной в период, а затем повторить построенный отрезок графика нужное число раз.

Примеры: функции и имеют наименьший положительный период 2p, функции и имеют наименьший положительный период p.