
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типы точек разрыва функции
Определение 5. Точка 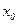 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции  , если левый и правый пределы
, если левый и правый пределы  при
при  конечные и равные, но не равны значению функции в точке
конечные и равные, но не равны значению функции в точке 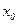 :
:  .
.
Определение 6. Точка  называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции  , если левый и правый пределы
, если левый и правый пределы  при
при  конечные, но не равны между собой:
конечные, но не равны между собой:  .
.
Определение 7. Точка  называется точкой разрыва второго рода функции f
называется точкой разрыва второго рода функции f  , если хотя бы один из односторонних пределов
, если хотя бы один из односторонних пределов  при
при  является бесконечным:
является бесконечным:  или (и)
или (и)  .
.
Пример 2. Исследовать на непрерывность и точки разрыва функцию
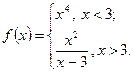
Решение. Так как на промежутках  и
и  данная функция совпадает с непрерывными функциями
данная функция совпадает с непрерывными функциями  и
и  , то она непрерывна на этих промежутках.
, то она непрерывна на этих промежутках.
Чтобы установить, является ли точка  точкой разрыва, и определить тип разрыва, вычислим пределы:
точкой разрыва, и определить тип разрыва, вычислим пределы:
 ,
,  .
.
Так как  , то точка
, то точка  является точкой разрыва второго рода функции
является точкой разрыва второго рода функции  .
.
Ответ. На промежутках  и
и  данная функция непрерывна;
данная функция непрерывна;  – точка устранимого разрыва;
– точка устранимого разрыва;  – точка разрыва второго рода.
– точка разрыва второго рода.
Пример 3. Исследовать на непрерывность и точки разрыва функцию
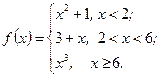
Решение. Так как на промежутках  ,
, 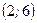 и
и  данная функция совпадает с непрерывными функциями
данная функция совпадает с непрерывными функциями  ,
,  и
и  , то она непрерывна на этих промежутках.
, то она непрерывна на этих промежутках.
Чтобы установить, являются ли точки 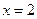 и
и  точками разрыва, и определить тип разрыва, вычислим пределы:
точками разрыва, и определить тип разрыва, вычислим пределы:
 ,
,  .
.
Так как значение  не определено, то
не определено, то  , следовательно, точка
, следовательно, точка 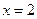 является точкой устранимого разрыва функции
является точкой устранимого разрыва функции  .
.
 ,
,  .
.
Так как левый и правый пределы  при
при  конечные и
конечные и  , то точка
, то точка  является точкой разрыва первого рода функции
является точкой разрыва первого рода функции  .
.
Ответ. На промежутках  ,
, 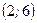 и
и  данная функция непрерывна;
данная функция непрерывна; 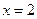 – точка устранимого разрыва;
– точка устранимого разрыва;  – точка разрыва первого рода.
– точка разрыва первого рода.
Пример 4. Исследовать на непрерывность и точки разрыва функцию
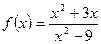
Решение. Так как функции  и
и 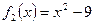 непрерывны при
непрерывны при  и
и  при
при  и
и  , то на промежутках
, то на промежутках  ,
,  и
и  данная функция непрерывна.
данная функция непрерывна.
Точки  и
и  являются точками разрыва, так как в этих точках данная функция не определена.
являются точками разрыва, так как в этих точках данная функция не определена.
Чтобы определить тип разрыва, вычислим пределы:
 ,
,  .
.
Так как значение  не определено, то
не определено, то  , то точка
, то точка  является точкой устранимого разрыва функции
является точкой устранимого разрыва функции  .
.
 (при
(при  выполняются условия
выполняются условия  и
и 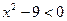 , поэтому
, поэтому  ).
).
 (при
(при  выполняются условия
выполняются условия  и
и  , поэтому
, поэтому  ).
).
Так как левый и правый пределы  при
при  бесконечные , то точка
бесконечные , то точка  является точкой разрыва второго рода функции
является точкой разрыва второго рода функции  .
.
Ответ. На промежутках  ,
,  и
и  данная функция непрерывна;
данная функция непрерывна;  – точка устранимого разрыва;
– точка устранимого разрыва;  – точка разрыва второго рода.
– точка разрыва второго рода.
Примеры вычисления пределов
1.  .
.
2.  .
.
3. 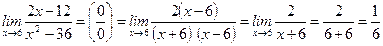
4.  .
.
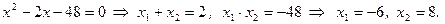
По формуле  получаем
получаем  Тогда
Тогда
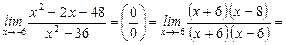
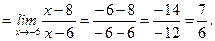
5.  .
.

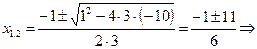




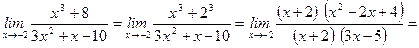
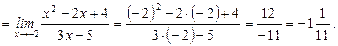
5. 

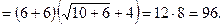
6. 



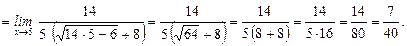
7.  .
.
8.  .
.
9.  .
.
10. 
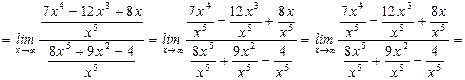
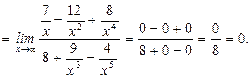
11. 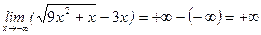
12. 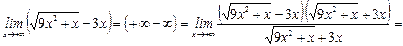
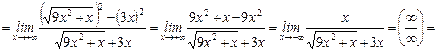
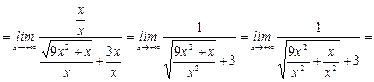
 .
.
13.  .
.
14. 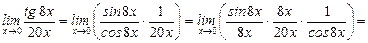
 .
.
15. 
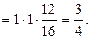
16. 
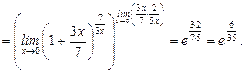
Дата добавления: 2015-04-18; просмотров: 360; Мы поможем в написании вашей работы!; Нарушение авторских прав |