Зависимость между ними

Определение 1. Функция называется бесконечно малой при , если .

Определение 2. Функция называется бесконечно малой при , если .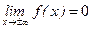

Определение 3. Функция называется бесконечно большой при , если для всех значений х, достаточно близких к , но не равных , функция принимает значения, как угодно большие по абсолютной величине.

Обозначение: .

Определение 4. Функция называется бесконечно большой при , если для всех достаточно больших значений х функция принимает значения, как угодно большие по абсолютной величине.

Определение 5. Функция называется бесконечно большой при , если для всех достаточно больших по абсолютной величине отрицательных значений х функция принимает значения, как угодно большие по абсолютной величине.

Обозначение: или .

Теорема 1. Если функция является бесконечно малой при , то функция является бесконечно большой при (то есть если , то ).

Теорема 2. Если функция является бесконечно большой при , то функция является бесконечно малой при (то есть если , то ).