
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Действия над комплексными числами в тригонометрической и показательной формах
1. При умножении комплексных чисел в тригонометрической или показательной форме модули этих чисел нужно перемножить, а аргументы сложить:
 ;
;
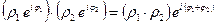 .
.
2. При делении комплексных чисел в тригонометрической или показательной форме нужно модуль делимого разделить на модуль делителя и из аргумента делимого вычесть аргумент делителя:
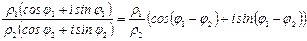 ;
;
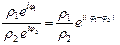
3. При возведении комплексного числа в степень в тригонометрической или показательной форме нужно модуль числа возвести в эту степень, а аргумент умножить на показатель степени.
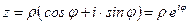

 .
.
Замечание. Умножение, деление и возведение в степень комплексных чисел в показательной форме производятся так же, как умножение, деление и возведение в степень степеней, что делает показательную форму комплексных чисел особенно удобной для выполнения этих действий.
Пример 14. Вычислить произведение и частное чисел 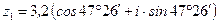 и
и

Решение
 .
.
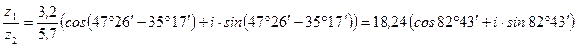 .
.
Ответ:  ,
,  .
.
Пример 15. Вычислить: 
Решение.  .
.
Ответ: 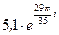 .
.
Пример 16. Вычислить:  .
.
Решение. 
Ответ:  .
.
Пример 17. Вычислить:  .
.
Решение.  .
.
Ответ:  .
.
Пример 18. Вычислить:  .
.
Решение. 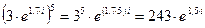
Ответ:
Пример 19. Вычислить  .
.
Решение. Представим основание степени в показательной форме. Так как  , то
, то  .
.
Так как  ,
,  , то
, то  (см. таблицу 1). Получаем:
(см. таблицу 1). Получаем:
 . Тогда
. Тогда  , поэтому
, поэтому
 .
.
Теперь представим результат в алгебраической форме.

 .
.
Ответ: 
Указание. Если в результате произведенных действий получается число, аргумент которого не удовлетворяет условию  , то нужно прибавить к нему (или вычесть из него)
, то нужно прибавить к нему (или вычесть из него)  столько раз, чтобы нужное условие выполнилось.
столько раз, чтобы нужное условие выполнилось.
Дата добавления: 2015-04-18; просмотров: 387; Мы поможем в написании вашей работы!; Нарушение авторских прав |