Геометрическое представление комплексных чисел

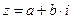Комплексное число можноизобразить на координатной плоскости в виде точки 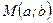или вектора .

Определение 9. Длина вектора, изображающего комплексное число , называется модулем комплексного числа и обозначается .

Определение 10. Величина направленного угла между осью абсцисс и вектором , изображающим комплексное число, называется аргументом комплексного числа и обозначается .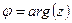

Замечание. Если угол – один из аргументов числа , то любой угол вида тоже является аргументом числа . Поэтому для определенности в дальнейшем будем считать, что .

Если даны модуль и аргумент комплексного числа, то его действительную и мнимую части можно найти по формулам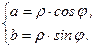

Если даны действительная и мнимая части комплексного числа, то его модуль можно найти по формуле , а аргумент –по его координатной четверти и по значению одной из его тригонометрических функций: , , .

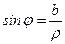Аргумент комплексного числа 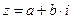можно найти также с помощью таблицы 1.

Таблица 1. Вычисление аргумента комплексного числа

Знак	Знак	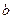Формула для вычисления аргумента	Знак	Знак	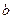Формула для вычисления аргумента

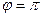
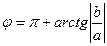
Пример 9. Найти модуль и аргумент комплексного числа .

Решение. Из условия находим: , .

Тогда по формуле получаем .

Так как и , то по таблице 1 находим формулу .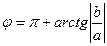

Тогда .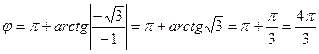

Ответ: , .

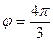Пример 10. Найти действительную и мнимую части комплексного числа, зная его модуль и аргумент .

Решение. По формулам находим:

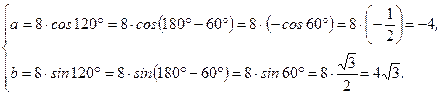
Ответ: , .