
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение 4. Суммой комплексных чисел и называется число .
Пример 3.  .
.
Определение 5. Разностью комплексных чисел  и
и  называется комплексное число
называется комплексное число  , которое в сумме с вычитаемым дает уменьшаемое:
, которое в сумме с вычитаемым дает уменьшаемое:  .
.
Можно доказать, что разность комплексных чисел  и
и  вычисляется по правилу
вычисляется по правилу  .
.
Пример 4.  .
.
Определение 6. Произведением комплексных чисел  и
и  называется комплексное число
называется комплексное число  .
.
Пример 5. 
Определение 7.Отношением комплексных чисел  и
и 
 называется комплексное число
называется комплексное число  , которое в произведении с делителем дает делимое:
, которое в произведении с делителем дает делимое:  .
.
Пример 6. Вычислить отношение  .
.
Так как искомое отношение является комплексным числом, то обозначим его так:
 .
.
Из определения 7 следует, что  .
.
Перемножив числа в правой части равенства, получаем:  .
.
Согласно определению 3, это уравнение равносильно системе уравнений:

Решим эту систему по формулам Крамера.
 ,
, 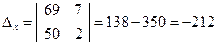 ,
, 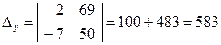 .
.
 ,
,  .
.
Окончательно получаем:  , что полностью соответствует вычислениям в примере 5:
, что полностью соответствует вычислениям в примере 5: 
Определение 8. Комплексное число 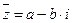 называется сопряженным комплексному числу
называется сопряженным комплексному числу 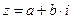 .
.
Замечание.Так как  , то числа
, то числа 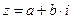 и
и 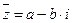 обычно называют взаимно сопряженными.
обычно называют взаимно сопряженными.
Пример 7. а)  ; б)
; б) 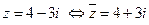 ;
;
в)  ; г)
; г) 
д)  ;
;
е)  .
.
Вычислим произведение взаимно сопряженных комплексных чисел:
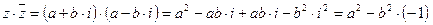 , или
, или  .
.
Таким образом, произведение взаимно сопряженных комплексных чисел является действительным (и даже положительным при  ) числом.
) числом.
Это свойство позволяет более удобным способом, чем по определению, находить отношение комплексных чисел. При делении комплексных чисел лучше сначала умножить делимое и делитель на число, сопряженное делителю, а затем произвести деление:
 .
.
Пример 8. Вычислим еще раз отношение  , используя свойство сопряженных чисел:
, используя свойство сопряженных чисел:

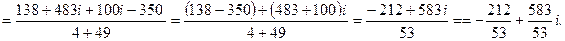
Окончательно получаем: 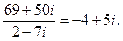
Практические рекомендации:
Сумму, разность и произведение комплексных чисел можно найти так же, как сумму, разность и произведение многочленов, учитывая только, что  .
.
При делении комплексных чисел удобнее сначала умножить делимое и делитель на число, сопряженное делителю, а затем уже выполнить деление.
Дата добавления: 2015-04-18; просмотров: 291; Мы поможем в написании вашей работы!; Нарушение авторских прав |