
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матрицы. Действия над матрицами, их свойства
Программы экзамена по математике за 3 семестр
Матрицы. Действия над матрицами, их свойства
Определение 1. Матрицей размерности m*n называется прямоугольная таблица, содержащая m*n чисел  , расположенных в m строках и n столбцах.
, расположенных в m строках и n столбцах.
Обозначение:  или
или  .
.
Числа  называются элементами матрицы. Числа
называются элементами матрицы. Числа  и
и  называются индексами элемента
называются индексами элемента  ;
;  ‒ номер строки,
‒ номер строки,  ‒ номер столбца, на пересечении которых расположен элемент
‒ номер столбца, на пересечении которых расположен элемент  ;
;  ;
;  .
.
Если  , то матрица называется квадратной матрицей порядка n.
, то матрица называется квадратной матрицей порядка n.
Определение 2.Матрицы  и
и 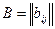 называются равными, если они имеют одинаковые размерности m*n и их одинаково расположенные элементы попарно равны, то есть
называются равными, если они имеют одинаковые размерности m*n и их одинаково расположенные элементы попарно равны, то есть 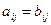 (
(  ;
;  ).
).
Пример 1. 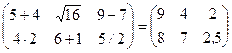 .
.
Определение 3.Суммой матриц  и
и 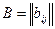 одинаковой размерности называется матрица
одинаковой размерности называется матрица  такой же размерности, элементы которой равны суммам соответствующих элементов данных матриц:
такой же размерности, элементы которой равны суммам соответствующих элементов данных матриц:
 (
(  ;
;  ).
).
Пример 2. 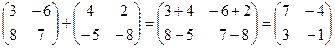 .
.
Определение 4.Произведением матрицы A на число k называется матрица B, каждый элемент которой равен произведению соответствующего элемента матрицы A на число k:
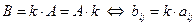 (
(  ;
;  ).
).
Пример 3. 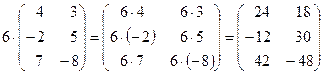 .
.
Определение 5.Пусть матрица  имеет размерность m*n, а матрица
имеет размерность m*n, а матрица 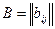 имеет размерность n*p. Произведением матриц A и B называется матрица
имеет размерность n*p. Произведением матриц A и B называется матрица 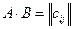 размерности m*p, каждый элемент
размерности m*p, каждый элемент  которой вычисляется по формуле
которой вычисляется по формуле
 (
(  ,
,  ).
).
Замечание. Чтобы матрицу A можно было умножить на матрицу B, число столбцов матрицы A обязательно должно быть равно числу строк матрицы B. Количество строк матрицы 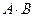 равно количеству строк матрицы А, количество столбцов матрицы
равно количеству строк матрицы А, количество столбцов матрицы 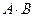 равно количеству столбцов матрицы B. Каждый элемент
равно количеству столбцов матрицы B. Каждый элемент  , расположенный на пересечении i-й строки и j-го столбца матрицы C, равен сумме произведений элементов i-й строки матрицы A и j-го столбца матрицы B.
, расположенный на пересечении i-й строки и j-го столбца матрицы C, равен сумме произведений элементов i-й строки матрицы A и j-го столбца матрицы B.
Пример 4.Пусть  ,
, 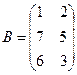 . Тогда
. Тогда
 .
.
Замечание. В данном случае произведение  не определено, так как количество столбцов матрицы B не равно количеству строк матрицы A.
не определено, так как количество столбцов матрицы B не равно количеству строк матрицы A.
Пример 5.  ,
,  .
.
Так как A и B ‒ квадратные матрицы одного порядка, то можно найти и произведение  , и произведение
, и произведение  .
.
 ,
,
 .
.
В данном примере 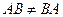 , то есть умножение матриц, вообще говоря, не коммутативно (не обладает свойством переместительности). Но в некоторых случаях равенство
, то есть умножение матриц, вообще говоря, не коммутативно (не обладает свойством переместительности). Но в некоторых случаях равенство  бывает верным. В таких случаях матрицы называются перестановочными.
бывает верным. В таких случаях матрицы называются перестановочными.
Пример 6.  ,
,  .
.
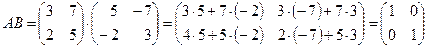 ,
,
 .
.
В данном случае матрицы A и B являются перестановочными.
Замечание 1. Матрица  называется единичной матрицей второго порядка. При умножении матриц единичная матрица играет такую же роль, как число 1 при умножении чисел (убедитесь сами, что
называется единичной матрицей второго порядка. При умножении матриц единичная матрица играет такую же роль, как число 1 при умножении чисел (убедитесь сами, что  ).
).
Матрицы, произведение которых равно единичной матрице, называются взаимно обратными. Матрица, обратная матрице  , обозначается
, обозначается  . Согласно определению,
. Согласно определению,  .
.
В примере 6 матрицы A и B взаимно обратные, то есть  ,
, 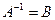 .
.
Замечание 2. Обратные матрицы используются, например, при решении систем линейных уравнений матричным методом.
Определение 6. Транспонированием матрицы называется операция, состоящая в замене строк матрицы ее столбцами, а столбцов строками.
Матрица, полученная транспонированием матрицы  , обозначается
, обозначается  .
.
Пример 7. 

 .
.
Пример 8. 

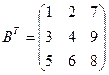 .
.
Свойства операций над матрицами
1º.  2º.
2º. 
3º.  4º.
4º. 
5º.  6º.
6º. 
7º.  8º.
8º.  9º.
9º. 
10º.  11º.
11º. 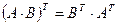
Дата добавления: 2015-04-18; просмотров: 405; Мы поможем в написании вашей работы!; Нарушение авторских прав |